题目内容
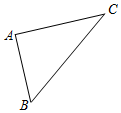
17.△ABC中,∠A=50°,两内角角平分线BD、CE交于点H,则∠BHC的度数为115°.分析 由三角形内角和可求得∠ABC+∠ACB,再由角平分线的定义可求得∠HBC+∠HCB,在△HBC中利用三角形内角和可求得∠BHC的度数.
解答 解:
∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵BD、CE分别平分∠ABC和∠ACB,
∴∠HBC+∠HCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×130°=65°,
∴∠BHC=180°-(∠HBC+∠HCB)=180°-65°=115°,
故答案为:115°.
点评 本题主要考查三角形内角和定理,利用三角形内角和定理和角平分线的定义求得∠HBC+∠HCB是解题的关键,注意整体思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
 如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
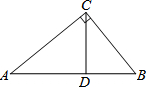 如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD=$\frac{1}{2}$.
如图所示,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD=$\frac{1}{2}$.
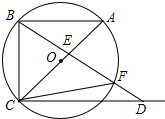 如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.
如图.点A、B、C为⊙O上三点,AC为⊙O的直径,AB∥CD,AC=CD.连接BD交AC于点E,交⊙O于点F,AB=$\sqrt{7}$,BC=3.