题目内容
3.如图,∠BAN=∠CAD=90°,∠B=∠ACD,BN=CD,点C在BN上.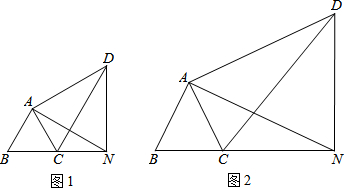
(1)当∠ANB=30°(如图1)时,∠DNB的度数是90°.
(2)当∠ANB≠30°(如图2)时,∠DNB的度数与(1)中的结果相同吗?请说明理由.
分析 (1)由△ABN≌△ACD,得到AN=AD,AB=AC,∠ADC=∠ANB=30°,证得△AND是等边三角形,即可得到结论.
(2)由(1)得△ABN≌△ACD,得AB=AC,AN=AD.又因为∠1+∠2=∠2+∠3=90°,得到∠1=∠3,得出△ABC∽△AND,证出∠B=∠AND,问题即可得证.
解答 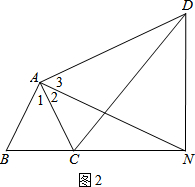 解:(1)在△ABN与△ACD中,
解:(1)在△ABN与△ACD中,
$\left\{\begin{array}{l}{∠B=∠ACD}\\{∠BAN=∠CAD}\\{BN=CD}\end{array}\right.$,
∴△ABN≌△ACD(AAS),
∴AN=AD,AB=AC,∠ADC=∠ANB=30°,
∴∠1=60°∠2=30°,
∴∠3=60°,
∴△AND是等边三角形,
∴∠AND=60°,
∴∠DNB=90°;
(2)相同,理由如下:
由(1)得△ABN≌△ACD,
得AB=AC,AN=AD.
又∵∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
∴△ABC∽△AND,
∴∠B=∠AND,
∵∠B+∠ANB=90°,
故∠DNB=∠AND+∠ANB=90°.
点评 本题考查了全等三角形的判定与性质,相似三角形的判定和性质,找准△ABC∽△AND是解题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
8. 在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
①起跑后1小时内,甲在乙的前面; ②第1小时两人都跑了10千米;
③甲比乙先到达终点; ④两人都跑了20千米.
正确的有( )
 在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:①起跑后1小时内,甲在乙的前面; ②第1小时两人都跑了10千米;
③甲比乙先到达终点; ④两人都跑了20千米.
正确的有( )
| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
12. 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
 如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )
如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为( )| A. | 6m2 | B. | 21m2 | C. | 3m2 | D. | 5m2 |
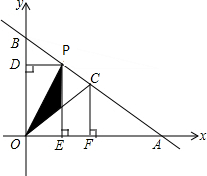 如图,点A,B坐标分别为(8,0)、(0,6),点C是线段AB的中点,点P是射线BA上一动点,过P作PD⊥y轴于D,PE⊥x轴于E,设OE=t,矩形OEPD与△POC重合部分的面积为S.
如图,点A,B坐标分别为(8,0)、(0,6),点C是线段AB的中点,点P是射线BA上一动点,过P作PD⊥y轴于D,PE⊥x轴于E,设OE=t,矩形OEPD与△POC重合部分的面积为S. 设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.
设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.