题目内容
4．一件工作，甲单独做15小时完成，乙单独做10小时完成，甲、乙先合做3小时候，因甲有其他任务调离，余下的任务由乙单独完成，求乙还需要多少小时才能完成？分析 把这项工作的工作总量看作单位“1”，则甲的工作效率为$\frac{1}{15}$，乙的工作效率为$\frac{1}{10}$，然后设乙还需要x小时才能完成，根据甲、乙先合做3小时的工作量+乙后单独完成x小时的工作量=工作总量“1”，列出方程解答即可．
解答 解：设乙还需要x小时才能完成，依题意有
（$\frac{1}{15}$+$\frac{1}{10}$）×3+$\frac{x}{10}$=1，
解得x=5．
答：设乙还需要5小时才能完成，
点评 此题考查了一元一次方程的应用，解题的关键是：根据题意找出等量关系：甲、乙先合做3小时的工作量+乙后单独完成x小时的工作量=工作总量“1”．
练习册系列答案
相关题目
12．
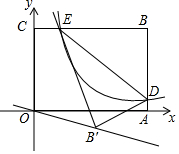如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数y=$\frac{6}{x}$的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（ ）
如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数y=$\frac{6}{x}$的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（ ）| A． | $-\frac{2}{5}$ | B． | $-\frac{1}{21}$ | C． | $-\frac{1}{5}$ | D． | $-\frac{1}{24}$ |
