题目内容
1．等腰三角形一条边的边长为3，它的另两条边的边长是关于x的一元二次方程x2-12x+k=0的两个根，则k的值是36．分析 分3为等腰三角形的腰与3为等腰三角形的底两种情况考虑，当3为等腰三角形的腰时，将x=3代入原方程可求出k的值，再利用分解因式法解一元二次方程可求出等腰三角形的底，由三角形的三边关系可确定此情况不存在；当3为等腰三角形的底时，由方程的系数结合根的判别式可得出△=144-4k=0，解之即可得出k值，进而可求出方程的解，再利用三角形的三边关系确定此种情况符合题意．此题得解．
解答 解：当3为等腰三角形的腰时，将x=3代入原方程得9-12×3+k=0，
解得：k=27，
此时原方程为x2-12x+27=（x-3）（x-9）=27，
解得：x1=3，x2=9，
∵3+3=6＜9，
∴3不能为等腰三角形的腰；
当3为等腰三角形的底时，方程x2-12x+k=0有两个相等的实数根，
∴△=（-12）2-4k=144-4k=0，
解得：k=36，
此时x1=x2=-$\frac{-12}{2}$=6，
∵3、6、6可以围成等腰三角形，
∴k=36．
故答案为：36．
点评 本题考查了根与系数的关系、根的判别式、三角形的三边关系以及等腰三角形的性质，分3为等腰三角形的腰与3为等腰三角形的底两种情况考虑是解题的关键．
练习册系列答案
相关题目
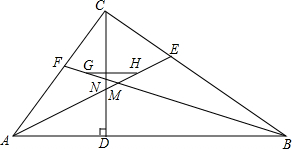如图Rt△ABC中，∠ACB=90°，AC=3，BC=4，CD⊥AB，AE、BF为角分线，CD与AE相交于M，BF、CD相交于N，H、G分别为EM、FN的中点，求GH的值．
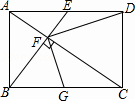在矩形ABCD中，点E为AD的中点，连接BE，AC，AC⊥BE于点F，连接DF，下列结论．①CF=2AF；②△DEF与△DFA相似；③∠DFC=∠BAC；④当G是BC中点时，有FG=DE，其中正确的个数是（ ）
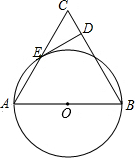在等边三角形△ABC中，以AB为直径的⊙O与AC交于点E，DE⊥BC于点D．
如图，正方形ABCD中，点P是BC边上的任意一点（异于端点B，C），连接AP，过点B，D两点作BE⊥AP于点E，DF⊥AP于点F．