题目内容
12．若△ABC∽△A′B′C′，且△ABC与△A′B′C′的相似比是1：2，已知△ABC的周长是3，则△A′B′C′的周长是（ ）| A． | 3 | B． | 6 | C． | 9 | D． | 12 |
分析 根据相似三角形的周长的比等于相似比得到△ABC的周长：△A′B′C′的周长=1：2，然后利用比例性质求解．
解答 解：∵△ABC∽△A′B′C′，
∴△ABC的周长：△A′B′C′的周长=1：2，
∴△A′B′C′的周长=2×3=6．
故选B．
点评 本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比；相似三角形的对应线段（对应中线、对应角平分线、对应边上的高）的比也等于相似比；相似三角形的面积的比等于相似比的平方．
练习册系列答案
相关题目
3．下列四个标志中，是轴对称图形的是图（ ）
| A． |  | B． |  | C． |  | D． |  |
20．不等式组$\left\{\begin{array}{l}{x+2＞0}\\{2x-1≤0}\end{array}\right.$的所有整数解是（ ）
| A． | -1、0 | B． | -2、-1 | C． | 0、1 | D． | -2、-1 |
7．若点M（m，n）（mn≠0）在二次函数y=ax2（a≠0）图象上，则下列坐标表示的点也在该抛物线图象上的是（ ）
| A． | （-m，n） | B． | （n，m） | C． | （m2，n2） | D． | （m，-n） |
4．
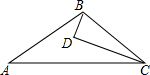如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）
如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）| A． | 1 | B． | 1.5 | C． | 2$\sqrt{2}$ | D． | 4 |
1．在△ABC中，如果AB=6，BC=10，那么AC的长可能是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 16 |
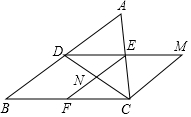如图，在三边互不相等的△ABC中，D、E、F分别是AB、AC、BC边的中点，连接DE，过点C作CM∥AB交DE的延长线于点M，连接CD、EF交于点N，则图中全等三角形共有（ ）