题目内容
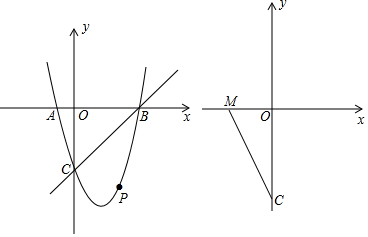
2.如图,抛物线y=ax2+bx-3的图象经过点A(-1,0),点B(3,0),与y轴交于点C,作直线BC.(1)求抛物线和直线CB的解析式;
(2)点P在直线BC下方的抛物线上,求点P到直线BC的距离的最大值;
(3)已知点M(-$\sqrt{3}$,0),连CM,点D为CM的中点,点Q在y轴上,连接MQ,将△QCD沿直线QD折叠得到△QED,当△QED与△MDQ重叠部分面积是△MCQ的面积的$\frac{1}{4}$时,直接写出所有符合条件的点Q的坐标.
分析 (1)利用待定系数法即可解决问题.
(2)设P(m,m2-2m-3),由题意当△PBC的面积最大时,点P到直线BC的距离的最大,构建二次函数,利用二次函数的性质即可解决问题.
(3)分两种情形①如图1中,当重叠部分是△OKD时,②如图2中,当重叠部分是△DKQ时,分别求解即可.
解答 解:(1)把A(-1,0),B(3,0)两点坐标代入y=ax2+bx-3得到$\left\{\begin{array}{l}{a-b-3=0}\\{9a+3b-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴抛物线的解析式为y=x2-2x-3,
∴C(0,-3),
设直线BC的解析式为y=kx+b则有$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴直线BC的解析式为 y=x-3.
(2)设P(m,m2-2m-3),
由题意当△PBC的面积最大时,点P到直线BC的距离的最大,
∵S△PBC=S△PCO+S△POB-S△BOC=$\frac{1}{2}$×3×m+$\frac{1}{2}$×3×(-m2+2m+3)-$\frac{1}{2}$×3×3=-$\frac{3}{2}$m2+$\frac{9}{2}$m=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,
∴当m=$\frac{3}{2}$时,△PBC的面积最大,最大值为$\frac{27}{8}$,设点P到BC的距离为h,
则有$\frac{1}{2}$×3$\sqrt{2}$×h=$\frac{27}{8}$,
∴h=$\frac{9\sqrt{2}}{8}$.
(3)①如图1中,当重叠部分是△OKD时,
在Rt△OCM中,∵∠MOC=90°,OM=$\sqrt{3}$,OC=3,
∴CM=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,tan∠OCM=$\frac{\sqrt{3}}{3}$,
∴∠MCO=30°
∵DM=DC,
∴OD=DM=DC=OM=$\sqrt{3}$,
∴∠DOC=∠DCO=30°,∠MOD=30°,
当点Q与O重合时,易知∠EOD=∠DOC=30°,
∴∠EOD=∠EOM=30°,
∴MK=KD,
∴S△OKD=$\frac{1}{4}$S△MOC.
此时Q(0,0).
②如图2中,当重叠部分是△DKQ时,
∵△QED与△MDQ重叠部分面积是△MCQ的面积的$\frac{1}{4}$,
∴MK=KQ,∵MD=DC,
∴ED∥OC,
∴∠QDE=∠DQC=∠QDC,
∴CD=CQ=$\sqrt{3}$,
∴Q(0,$\sqrt{3}$-3).
综上所述,当Q(0,0)或(0,$\sqrt{3}$-3)时,△QED与△MDQ重叠部分面积是△MCQ的面积的$\frac{1}{4}$.
点评 本题考查二次函数综合题、一次函数的应用、待定系数法、三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,注意一题多解,属于中考压轴题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案| A. | -4 | B. | 0 | C. | 1 | D. | 3 |
| A. | x≠1 | B. | x≠-1 | C. | x≥1 | D. | x≥-1 |
| A. | 2 | B. | -$\frac{1}{2}$ | C. | -2 | D. | $\frac{1}{2}$ |
| A. | -1 | B. | 3 | C. | -3 | D. | 3或-1 |
| A. | 5 | B. | -3 | C. | 5或-3 | D. | 以上都不对 |
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
| A. | 44°26′ | B. | 44°56′ | C. | 34°56′ | D. | 34°26′ |