题目内容
20.关于x的方程ax2+2(a-3)x+(a-2)=0至少有一个整数根,且a是整数,求a的值.分析 当a=0时化为一次方程求出x,当a≠0 时,方程为一元二次方程,由△=4(9-4a)为完全平方数知9-4a为完全平方数,设9-4a=n2,则n为正奇数且n≠3,知a=$\frac{9-{n}^{2}}{4}$,代入求根公式后根据方程有整数根判断即可.
解答 解:当a=0时,原方程为-6x-2=0,解得:x=-$\frac{1}{3}$,即原方程无整数解.
当a≠0 时,方程为一元二次方程,它至少有一个整数根,
∴△=[2(a-3)]2-4a(a-2)=4(9-4a)为完全平方数,即9-4a为完全平方数,
设9-4a=n2,则n为正奇数,且n≠3 否则a=0,
所以a=$\frac{9-{n}^{2}}{4}$,
由求根公式得:x=$\frac{-2(a-3)±2n}{2a}$=-1+$\frac{3±n}{a}$=-1+$\frac{4(3±n)}{9-{n}^{2}}$,
所以x1=-1+$\frac{4}{3+n}$,x2=-1+$\frac{4}{3-n}$,
要使x1为整数,而n为正奇数,只能n=1,从而a=2,
要使x2为整数,n可取1,5,7,从而a=2,-4,-10,
综上所述,a的值为2,-4,-10.
点评 本题主要考查一元二次方程根的判别式,熟练掌握根的判别式与求根公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若样本a1+1,a2+1,…,an+1的平均数为6,方差为1,则对于样本里a1+3,a2+3,…,an+3,下列结论正确的是( )
| A. | 平均数为6,方差为1 | B. | 平均数为6,方差为4 | ||
| C. | 平均数为8,方差为1 | D. | 平均数为8,方差为4 |
 已知矩形ABCD,AB=6,AD=4$\sqrt{3}$
已知矩形ABCD,AB=6,AD=4$\sqrt{3}$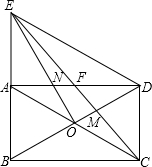 如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.
如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M. 如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).
如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).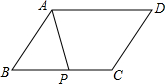 如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,
如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$, 由若干个相同的小正方体搭成的一个几何体如图所示,它的俯视图为( )
由若干个相同的小正方体搭成的一个几何体如图所示,它的俯视图为( )


