题目内容
要使多项式mx3+3nxy2+2x3-xy2+y不含三次项,求2m+3n的值.
考点:多项式
专题:
分析:根据多项式mx3+3nxy2+2x3-xy2+y不含三次项,得出m+2=0,3n-1=0,求出m,n的值,再代入计算即可.
解答:解:∵多项式mx3+3nxy2+2x3-xy2+y不含三次项,
∴m+2=0,3n-1=0,
∴m=-2,n=
∴2m+3n=2×(-2)+3×
=-3.
∴m+2=0,3n-1=0,
∴m=-2,n=
| 1 |
| 3 |
∴2m+3n=2×(-2)+3×
| 1 |
| 3 |
点评:此题主要考查了多项式的定义,利用多项式不含三次项得出三次项系数和为0进而求出是解题关键.

练习册系列答案
相关题目
若-ab<0且b<0,则2a+5|a|等于( )
| A、7a | B、-7a |
| C、3a | D、-3a |
已知|a+3|+|b-5|=0,则a、b的值为( )
| A、a=3,b=5 |
| B、a=-3,b=5 |
| C、a=-3,b=-5 |
| D、a=3,b=-5 |
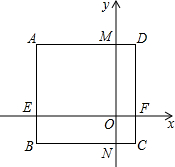 长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.
长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.