题目内容
3.在平面直角坐标系中,将点P(-1,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是( )| A. | (2,5) | B. | (1,5) | C. | (1,-3) | D. | (-5,5) |
分析 根据向右平移横坐标加,向上平移纵坐标加即可得解.
解答 解:将点P(-1,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是(-1+3,1+4),即(2,5).
故选A.
点评 本题考查了坐标与图形变化-平移,熟记平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.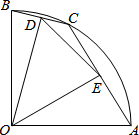 如图,在扇形OAB中,∠AOB=90°,点C是$\widehat{AB}$上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若DE=1,则扇形OAB的面积为( )
如图,在扇形OAB中,∠AOB=90°,点C是$\widehat{AB}$上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若DE=1,则扇形OAB的面积为( )
 如图,在扇形OAB中,∠AOB=90°,点C是$\widehat{AB}$上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若DE=1,则扇形OAB的面积为( )
如图,在扇形OAB中,∠AOB=90°,点C是$\widehat{AB}$上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若DE=1,则扇形OAB的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{2}{3}π$ | C. | π | D. | 2π |
18.若将抛物线y=$\frac{1}{2}$x2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的表达式是( )
| A. | $y=\frac{1}{2}{(x+2)^2}-1$ | B. | $y=\frac{1}{2}{(x-2)^2}-1$ | C. | y=(x+2)2-1 | D. | $y=\frac{1}{2}(x-2)+1$ |
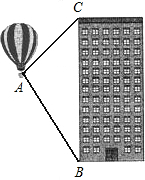 热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,这栋高楼的高是100米,A处与高楼的水平距离是50($\sqrt{3}$-1)米.
热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,这栋高楼的高是100米,A处与高楼的水平距离是50($\sqrt{3}$-1)米.