题目内容
11.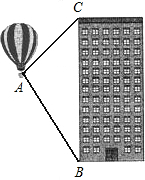 热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,这栋高楼的高是100米,A处与高楼的水平距离是50($\sqrt{3}$-1)米.
热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,这栋高楼的高是100米,A处与高楼的水平距离是50($\sqrt{3}$-1)米.
分析 作AD⊥BC于D,设AD=x米,根据等腰直角三角形的性质和正切的定义表示出CD、BD,根据题意列出方程,解方程即可.
解答 解: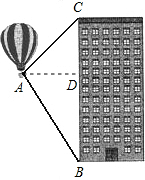 作AD⊥BC于D,
作AD⊥BC于D,
设AD=x米,
∵∠CAD=45°,
∴CD=AD=x,
∵∠BAD=60°,
∴BD=AD•tan∠BAD=$\sqrt{3}$x,
由题意得,$\sqrt{3}$x+x=100,
解得,x=50($\sqrt{3}$-1),
∴A处与高楼的水平距离50($\sqrt{3}$-1)米,
故答案为:50($\sqrt{3}$-1).
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
2.下列句子中,不是命题的是( )
| A. | 三角形的内角和等于180° | B. | 对顶角相等 | ||
| C. | 过一点作已知直线的平行线 | D. | 两点确定一条直线 |
3.在平面直角坐标系中,将点P(-1,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是( )
| A. | (2,5) | B. | (1,5) | C. | (1,-3) | D. | (-5,5) |
20. 某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
(1)表中m=500,n=0.05;
(2)在图中,将表示“自然科学”的部分补充完整;
(3)若该学校打算采购一万册图书,请你估算“哲学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.
 某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:| 各种图书 | 频数 | 频率 |
| 自然科学 | 400 | 0.20 |
| 文学艺术 | 1000 | 0.50 |
| 社会百科 | m | 0.25 |
| 哲学 | n |
(2)在图中,将表示“自然科学”的部分补充完整;
(3)若该学校打算采购一万册图书,请你估算“哲学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.
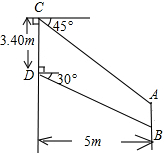 我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)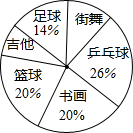 九(1)班全体同学根据自己的爱好参加了六个兴趣小组(每个学生必须参加且只参加一个),为了了解学生参加兴趣小组的情况,班主任参加各个兴趣小组的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“足球”小组的学生有7人,请解答下列问题:
九(1)班全体同学根据自己的爱好参加了六个兴趣小组(每个学生必须参加且只参加一个),为了了解学生参加兴趣小组的情况,班主任参加各个兴趣小组的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“足球”小组的学生有7人,请解答下列问题: 如图,直线y=kx+b与x轴交于点B(-3,0),且它与双曲线y=$\frac{12}{x}$交于点A、C,其中点A(n,4)在第一象限,点C在第三象限.
如图,直线y=kx+b与x轴交于点B(-3,0),且它与双曲线y=$\frac{12}{x}$交于点A、C,其中点A(n,4)在第一象限,点C在第三象限.