题目内容
16.某次军事演习中,有三艘军舰在同一时刻向指挥所报告.A舰说:“B舰在它的正东方向,C舰在它的北偏东方向”,B舰说:“C舰在它的北偏西30°方向”.C舰说:“它到A舰的距离比它到B舰的距离远40海里”.求A、B两舰的距离是多少海里(精确到0.1海里)?($\sqrt{2}$≈1.41.$\sqrt{3}$≈1.73.$\sqrt{6}$=2.45)分析 首先根据叙述作出图形,设BD=x海里,根据三角函数分别表示出BC、CD、AC、AD.根据C船说它在A船的距离比它到B船的距离远40海里,即AC-BC=40海里,即可列出方程,求得AB的距离.
解答 解:如图,
根据题意,∠CAD=45°,∠BCD=30°,
过点C作CD⊥AB于点D,设BD=x海里,
在RT△BCD中,∵∠BCD=30°,
∴BC=2x,CD=$\sqrt{B{C}^{2}-B{D}^{2}}=\sqrt{3}x$,
在RT△ACD中,∵∠CAD=45°,
∴AD=CD=$\sqrt{3}$x,AC=$\frac{CD}{sin∠CAD}=\frac{\sqrt{3}x}{\frac{\sqrt{2}}{2}}$=$\sqrt{6}$x,
又∵AC-BC=40,
∴$\sqrt{6}$x-2x=40,解得:x=20($\sqrt{6}$+2),
故AB=AD+BD=$\sqrt{3}$x+x=($\sqrt{3}$+1)×20($\sqrt{6}$+2)≈243.1(海里).
答:A、B两舰的距离约为243.1海里.
点评 本题主要考查了三角函数的应用,正确利用三角函数把求线段的长的问题转化为方程问题是解题的关键.

练习册系列答案
相关题目
6.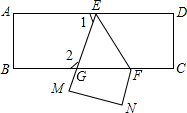 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )
 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )| A. | 105 | B. | 110 | C. | 95 | D. | 120 |
7.下列四个命题中,真命题是( )
| A. | 对角线互相垂直平分的四边形是正方形 | |
| B. | 对角线相等且互相平分的四边形是矩形 | |
| C. | 对角线垂直相等的四边形是菱形 | |
| D. | 四边都相等的四边形是正方形 |
11. 如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
 如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )
如图,这是某地2014年和2015年粮食作物产量的条形统计图,请你根据此图判断下列说法合理的是( )| A. | 2015年三类农作物的产量比2014年都有增加 | |
| B. | 玉米产量和杂粮产量增长率相当 | |
| C. | 2014年杂粮产量是玉米产量的约七分之一 | |
| D. | 2014年和2015年的小麦产量基本持平 |
20.计算|-5|+(π-3.14)0-($\frac{1}{2}$)-1的结果是( )
| A. | 0 | B. | 1 | C. | 4 | D. | 6.5 |
2.下列句子中,不是命题的是( )
| A. | 三角形的内角和等于180° | B. | 对顶角相等 | ||
| C. | 过一点作已知直线的平行线 | D. | 两点确定一条直线 |
3.在平面直角坐标系中,将点P(-1,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是( )
| A. | (2,5) | B. | (1,5) | C. | (1,-3) | D. | (-5,5) |
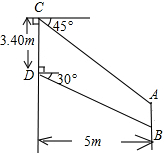 我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
我国某型号飞机的机翼形状如图所示,AB∥CD,根据图中所给数据计算这块机翼的面积(结果精确到0.01m2,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)