题目内容
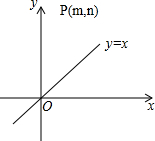 点P在第一象限,坐标为(m,n).
点P在第一象限,坐标为(m,n).(1)点Q是点P关于直线y=x的轴对称点,直接写出Q点坐标(用m、n表示);
(2)过Q作y轴平行线交直线y=x于A,若OQ2-AQ2=4,求经过点Q的双曲线的解析式;
(3)在(2)的条件下,若经过O、P、Q三点的抛物线的对称轴为x=
| 7 |
| 6 |
考点:反比例函数综合题
专题:
分析:(1)设Q是P的对称点,作PC⊥y轴于点C,PD⊥x轴于点D,易证△POC≌△QOD,据此即可求解;
(2)设双曲线为y=
,则Q(n,
),A(n,m).则OQ和都可以利用n和k表示出来,根据OQ2-AQ2=4,即可列方程求解;
(3)设抛物线的解析式是y=ax2+bx,把P和Q坐标代入,然后利用对称轴的公式,即可列方程组求解.
(2)设双曲线为y=
| k |
| x |
| k |
| n |
(3)设抛物线的解析式是y=ax2+bx,把P和Q坐标代入,然后利用对称轴的公式,即可列方程组求解.
解答: 解:(1)∵设Q是P的对称点,则直线y=x垂直平分PQ,连接OP、OQ,则OP=OQ,且直线y=x平分∠POQ,又y=x平分∠xOy.
解:(1)∵设Q是P的对称点,则直线y=x垂直平分PQ,连接OP、OQ,则OP=OQ,且直线y=x平分∠POQ,又y=x平分∠xOy.
∴∠xOQ=∠yOP,
作PC⊥y轴于点C,PD⊥x轴于点D.
则△POC≌△QOD,
∴OD=OC=n,QD=PC=m,
故点Q的坐标是(n,m);
(2)设双曲线为y=
,则Q(n,
),A(n,m).
∴AQ=n-
,
∴OQ2-AQ2=n2+(
)2-(n-
)2,
∴2k=4,
∴k=2,
∴反比例函数的解析式是:y=
;
(3)∵抛物线经过原点,
∴设抛物线的解析式是y=ax2+bx,
则
,
得:
,
又∵-
=
,
∴
=
=
,
即
=
,
3(m+
)2-7(m+
)-6=0,
则m+
=3…1)或m+
=-
…2),
解1)得:m=1或2,方程2)无解.
故P的坐标是(1,2)或(2,1).
 解:(1)∵设Q是P的对称点,则直线y=x垂直平分PQ,连接OP、OQ,则OP=OQ,且直线y=x平分∠POQ,又y=x平分∠xOy.
解:(1)∵设Q是P的对称点,则直线y=x垂直平分PQ,连接OP、OQ,则OP=OQ,且直线y=x平分∠POQ,又y=x平分∠xOy.∴∠xOQ=∠yOP,
作PC⊥y轴于点C,PD⊥x轴于点D.
则△POC≌△QOD,
∴OD=OC=n,QD=PC=m,
故点Q的坐标是(n,m);
(2)设双曲线为y=
| k |
| x |
| k |
| n |
∴AQ=n-
| k |
| n |
∴OQ2-AQ2=n2+(
| k |
| n |
| k |
| n |
∴2k=4,
∴k=2,
∴反比例函数的解析式是:y=
| 2 |
| x |
(3)∵抛物线经过原点,
∴设抛物线的解析式是y=ax2+bx,
则
|
得:
|
又∵-
| b |
| 2a |
| 7 |
| 6 |
∴
| ||||
2(-
|
| ||||
|
| 7 |
| 6 |
即
| ||||
m+
|
| 7 |
| 6 |
3(m+
| 2 |
| m |
| 2 |
| m |
则m+
| 2 |
| m |
| 2 |
| m |
| 2 |
| 3 |
解1)得:m=1或2,方程2)无解.
故P的坐标是(1,2)或(2,1).
点评:本题考查了待定系数法求函数的解析式,以及全等三角形的判定与性质,正确解方程组是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
二次函数y=x2+2的图象大致是( )
A、 |
B、 |
C、 |
D、 |
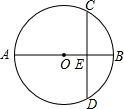 如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=8,BE=2,则⊙O的直径为
如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=8,BE=2,则⊙O的直径为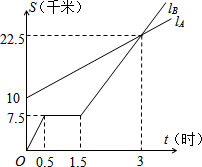 如图,lA与 lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.B自行车遇到故障中途停下修理1小时.若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?
如图,lA与 lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.B自行车遇到故障中途停下修理1小时.若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?