题目内容
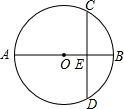 如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=8,BE=2,则⊙O的直径为
如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=8,BE=2,则⊙O的直径为考点:垂径定理,勾股定理
专题:计算题
分析:连结OC,如图,设⊙O的半径为r,则OE=r-2,根据垂径定理,由CD⊥AB得到CE=
CD=4,然后在Rt△OCE中利用勾股定理得(r-2)2+42=r2,解方程得r=5,即可得到⊙O的直径为10.
| 1 |
| 2 |
解答:解:连结OC,如图, 设⊙O的半径为r,则OE=OB-BE=r-2,
设⊙O的半径为r,则OE=OB-BE=r-2,
∵CD⊥AB,
∴CE=DE=
CD=4,
在Rt△OCE中,∵OE2+CE2=OC2,
∴(r-2)2+42=r2,解得r=5,
∴⊙O的直径为10.
故答案为10.
 设⊙O的半径为r,则OE=OB-BE=r-2,
设⊙O的半径为r,则OE=OB-BE=r-2,∵CD⊥AB,
∴CE=DE=
| 1 |
| 2 |
在Rt△OCE中,∵OE2+CE2=OC2,
∴(r-2)2+42=r2,解得r=5,
∴⊙O的直径为10.
故答案为10.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目
若单项式
x2yn与-2xmy3是同类项,则m-n的值是( )
| 2 |
| 3 |
| A、2 | B、1 | C、-1 | D、-2 |
在同一直角坐标系中,函数y=bx-a和y=ax-b的图象可能是( )
A、 |
B、 |
C、 |
D、 |
若点P(1,-n),Q(m,3)关于原点对称,则P,Q两点的距离为( )
| A、8 | ||
B、2
| ||
C、
| ||
D、2
|
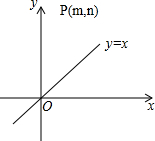 点P在第一象限,坐标为(m,n).
点P在第一象限,坐标为(m,n).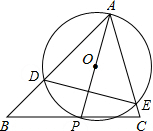 如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2
如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2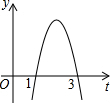 二次函数y=ax2+bx+c的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;③abc<0;④4ac-b2<0,其中正确的有( )个.
二次函数y=ax2+bx+c的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;③abc<0;④4ac-b2<0,其中正确的有( )个.