题目内容
4.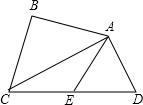 如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=1,AC=$\sqrt{2}$,点E为CD中点.求证:CD=2AE.
如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=1,AC=$\sqrt{2}$,点E为CD中点.求证:CD=2AE.
分析 首先利用已知条件和勾股定理可证明BC=AB,进而可得∠BCA=∠BAC=45°,再根据已知条件可得∠CAD=135-45°=90°,所以三角形CAD是直角三角形,利用在直角三角形中,斜边上的中线等于斜边的一半即可证明CD=2AE.
解答 证明:Rt△ABC中,∠ABC=90°,
AB=1,AC=$\sqrt{2}$
∴BC2=($\sqrt{2}$)2-12=1,
∴BC=AB,
∴∠BCA=∠BAC=45°,
又∵∠BAD=135°,
∴∠CAD=135-45°=90°,
又∵AE为CD上中点,
∴AE为Rt△CAD斜边上中线,则CD=2AE.
点评 本题考查了勾股定理的运用以及在直角三角形中,斜边上的中线等于斜边的一半.(即直角三角形的外心位于斜边的中点)的性质,解题的关键是证明△CAD是直角三角形.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
15.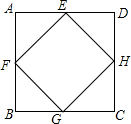 如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
 如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )
如图,点E、F、G、H是正方形ABCD各边的中点,则四边形EFGH( )| A. | 是轴对称图形但不是中心对称图形 | B. | 既是轴对称图形又是中心对称图形 | ||
| C. | 是中心对称图形但不是轴对称图形 | D. | 没有对称性 |
19.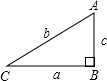 如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
 如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )| A. | a2+b2=c2 | B. | a2+c2=b2 | C. | b2+c2=a2 | D. | (a+c)2=b2 |
16.代数式$\frac{\sqrt{x-5}}{x-6}$有意义,则x的取值范围是( )
| A. | x≤5 | B. | x≥5 | C. | x>5且x≠6 | D. | x≥5且x≠6 |
13.某商场用18万元购进A、B两种商品,其进价和售价如下表:
(1)若销售完后共获利3万元,该商场购进A、B两种商品各多少件;
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?
| A | B | |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1380 | 1200 |
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
①问共有几种进货方案?
②要保证利润最高,你选择哪种进货方案?