题目内容
3.(1)计算:$\sqrt{8}$×sin45°-($\frac{1}{2}$)-2+|-3|(2)化简,求值:($\frac{1}{x+2}$+1)÷$\frac{{x}^{2}-9}{{x}^{2}+4x+4}$,其中x=4.
分析 (1)首先化简二次根式,计算负指数次幂以及去掉绝对值符号,然后进行加减即可;
(2)首先对括号内的分式通分相加,把除法转化为乘法,然后计算乘法即可化简,最后代入数值计算即可.
解答 解:(1)原式=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-4+3=2-4+3=1;
(2)原式=$\frac{1+x+2}{x+2}$÷$\frac{(x+3)(x-3)}{(x+2)^{2}}$
=$\frac{x+3}{x+2}$•$\frac{(x+2)^{2}}{(x+3)(x-3)}$
=$\frac{x+2}{x-3}$.
当x=4时,原式=6.
点评 本题考查了实数的混合运算以及分式的化简求值,正确对分式进行通分、约分是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.抛物线$y=-\frac{1}{2}{x^2}$不具有的性质是( )
| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 函数有最小值 |
 如图,每个小正方形的边长为1个单位
如图,每个小正方形的边长为1个单位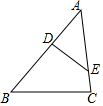 如图,在△ABC的边AB、AC上有点D、E.若∠BDE+∠C=180°,求证:$\frac{AD}{AC}$=$\frac{AE}{AB}$.
如图,在△ABC的边AB、AC上有点D、E.若∠BDE+∠C=180°,求证:$\frac{AD}{AC}$=$\frac{AE}{AB}$. 如图,四边形ABCD是矩形(AD>AB),请用直尺和圆规在边AD上找一点P,使得BP=2AB.(不写作法,保留作图痕迹)
如图,四边形ABCD是矩形(AD>AB),请用直尺和圆规在边AD上找一点P,使得BP=2AB.(不写作法,保留作图痕迹)