题目内容
14.为了响应“足球进校园”的号召,某校计划为校足球队购置一批足球.已知购买2个甲型足球和3个乙型足球共需380元;购买4个甲型足球和2个乙型足球共需360元.(1)求甲,乙两种型号足球的单价;
(2)该校共购买甲、乙两种型号足球10个,设购买甲型足球x个,所需总费用为y元,求y与x之间的函数解析式,并写出x的取值范围;
(3)若购买的10个足球中要求甲型不超过乙型的一半,求该校购买10个足球的最小费用.
分析 (1)设甲型足球的单价为m元/个,乙型足球的单价为n元/个,根据“购买2个甲型足球和3个乙型足球共需380元;购买4个甲型足球和2个乙型足球共需360元”,即可得出关于m、n的二元一次方程组,解之即可得出结论;
(2)设购买甲型足球x个,所需总费用为y元,则购买乙型足球(10-x)个,根据总费用=甲型足球单价×购买数量+乙型足球单价×购买数量,即可得出y与x之间的函数解析式;
(3)根据购买的10个足球中要求甲型不超过乙型的一半,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再根据一次函数的性质即可解决最值问题.
解答 解:(1)设甲型足球的单价为m元/个,乙型足球的单价为n元/个,
根据题意得:$\left\{\begin{array}{l}{2m+3n=380}\\{4m+2n=360}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=40}\\{n=100}\end{array}\right.$.
答:甲型足球的单价为40元/个,乙型足球的单价为100元/个.
(2)设购买甲型足球x个,所需总费用为y元,则购买乙型足球(10-x)个,
根据题意得:y=40x+100(10-x)=-60x+1000(0≤x≤10,且x为整数).
(3)根据题意得:x≤$\frac{1}{2}$(10-x),
解得:x≤$\frac{10}{3}$,
∵x为整数,
∴x≤3.
∵在y=-60x+1000中,-60<0,
∴当x=3时,y取最小值,最小值为820.
∴当购买甲型足球3个、乙型足球7个时,该校购买10个足球的费用最低,最低费用为820元.
点评 本题考查了一次函数的应用、二元一次方程的应用、一次函数的性质以及解一元一次不等式,解题的关键是:(1)找准等量关系,列出二元一次方程组;(2)根据总费用=甲型足球单价×购买数量+乙型足球单价×购买数量,找出y与x之间的函数解析式;(3)根据一次函数的性质,解决最值问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案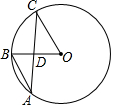 如图,点B是⊙O的劣弧$\widehat{AC}$上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( )
如图,点B是⊙O的劣弧$\widehat{AC}$上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( )| A. | 81° | B. | 72° | C. | 60° | D. | 63° |
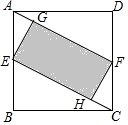 如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在正方形ABCD中,E、F分别是AB、CD的中点,EG⊥AF,FH⊥CE,垂足分别为G,H,设AG=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )| A. | y=3$\sqrt{3}$x2 | B. | y=4$\sqrt{3}$x2 | C. | y=8x2 | D. | y=9x2 |
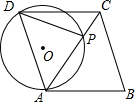 如图,点P在菱形ABCD的对角线AC上,PA=PD,⊙O为△APD的外接圆.
如图,点P在菱形ABCD的对角线AC上,PA=PD,⊙O为△APD的外接圆. 在?ABCD中,∠BAD的平分线AE交BC于点E,BE=3,若?ABCD的周长是16,则EC=2.
在?ABCD中,∠BAD的平分线AE交BC于点E,BE=3,若?ABCD的周长是16,则EC=2. 如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,DE⊥AB,则∠ABE的度数为36°.
如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,DE⊥AB,则∠ABE的度数为36°. 如图,圆锥的底面半径为9cm,母线长为30cm,这个圆锥的侧面积为270πcm2.
如图,圆锥的底面半径为9cm,母线长为30cm,这个圆锥的侧面积为270πcm2.