题目内容
4.某中商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3120元,问第一次降价后至少要售出该种商品多少件?
分析 (1)设该种商品每次降价的百分率为x%,根据“两次降价后的售价=原价×(1-降价百分比)的平方”,即可得出关于x的一元二次方程,解方程即可得出结论;
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品(100-m)件,根据“总利润=第一次降价后的单件利润×销售数量+第二次降价后的单件利润×销售数量”,即可得出关于m的一元一次不等式,解不等式即可得出结论.
解答 解:(1)设该种商品每次降价的百分率为x%,
依题意得:400×(1-x%)2=324,
解得:x=10,或x=190(舍去).
答:该种商品每次降价的百分率为10%.
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品(100-m)件,
第一次降价后的单件利润为:400×(1-10%)-300=60(元/件);
第二次降价后的单件利润为:324-300=24(元/件).
依题意得:60m+24×(100-m)=36m+2400≥3120,
解得:m≥20.
答:为使两次降价销售的总利润不少于3120元.第一次降价后至少要售出该种商品20件.
点评 本题考查了一元二次方程的应用以及一元一次不等式的应用,解题的关键是:(1)根据数量关系得出关于x的一元二次方程;(2)根据数量关系得出关于m的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出不等式(方程或方程组)是关键.

练习册系列答案
相关题目
15.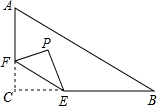 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )| A. | 3.2 | B. | 2 | C. | 1.2 | D. | 1 |
19.将不等式4x-3<1的解集表示在数轴上,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
9.下列运算结果为2a3的是( )
| A. | a3•a3 | B. | 5a3-3a3 | C. | 2a6÷a2 | D. | 5a5-3a2 |
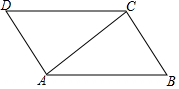 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线.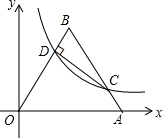 如图,正三角形△OAB的边OA在x轴上,D是OB边上的动点(不与端点O,B重合),双曲线y=$\frac{k}{x}$过点D,且与BA交于点C,设AB=8,$\frac{BD}{BO}$=n.
如图,正三角形△OAB的边OA在x轴上,D是OB边上的动点(不与端点O,B重合),双曲线y=$\frac{k}{x}$过点D,且与BA交于点C,设AB=8,$\frac{BD}{BO}$=n.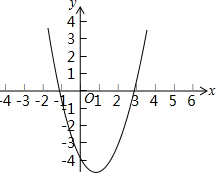 设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题: