题目内容
关于x的方程mx-6=3x的解为正实数,则m的取值范围是 .
考点:一元一次方程的解,解一元一次不等式
专题:
分析:先移项得mx-6=3x,再合并得(m-3)x=6,然后把x的系数化为1得x=
(m≠3)由于关于x的方程mx-6=3x的解为正实数,则x>0,即
>0,然后再解不等式即可.
| 6 |
| m-3 |
| 6 |
| m-3 |
解答:解:移项、合并同类项,得
(m-3)x=6,
系数化为1得x=
(m≠3),
∵关于x的方程mx-6=3x的解为正实数,
∴x>0,即
>0,
∴m-3>0,
∴m>3.
故答案是:m>3.
(m-3)x=6,
系数化为1得x=
| 6 |
| m-3 |
∵关于x的方程mx-6=3x的解为正实数,
∴x>0,即
| 6 |
| m-3 |
∴m-3>0,
∴m>3.
故答案是:m>3.
点评:本题考查了解一元一次方程:先去括号,再移项,把含未知数的项移到方程的左边,然后进行合并同类项后把未知数的系数化为1即可得到方程的解.也考查了解一元一次不等式.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
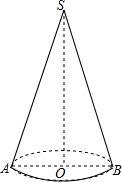 如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径,已知SA=7cm,AB=4cm,求截面△SAB的面积.
如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径,已知SA=7cm,AB=4cm,求截面△SAB的面积.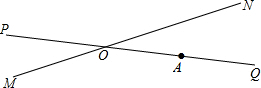 铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=300m,如果火车行驶时,周围250m以内都会受到噪音的影响,那么火车在铁路MN沿ON方向行驶时,居民楼是否会受到噪音的影响?请说明理由.如果火车行驶的速度是72km/h,居民楼受噪音影响的时间约为多少秒?(提示:过点A作MN的垂线段AC)
铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=300m,如果火车行驶时,周围250m以内都会受到噪音的影响,那么火车在铁路MN沿ON方向行驶时,居民楼是否会受到噪音的影响?请说明理由.如果火车行驶的速度是72km/h,居民楼受噪音影响的时间约为多少秒?(提示:过点A作MN的垂线段AC) 如图,三点A,B,D在数轴上,点A,B在数轴上表示问数分别为-12,16(设定:数轴上A,B之间的距离记为AB)
如图,三点A,B,D在数轴上,点A,B在数轴上表示问数分别为-12,16(设定:数轴上A,B之间的距离记为AB)