题目内容
13．抛物线y=x2-4x+c与x轴交于A、B两点，已知点A的坐标为（1，0），则线段AB的长度为2．分析 首先求出抛物线y=x2-4x+c对称轴，然后根据二次函数图象的对称性求出点B的坐标，进而求出线段AB的长度．
解答 解：∵抛物线y=x2-4x+c=（x-2）2-4+c，
∴抛物线的对称轴为直线x=2，
∵点A的坐标为（1，0），
∴点B的坐标为（3，0），
∴线段AB=3-1=2，
故答案为2．
点评 本题主要考查了抛物线与x轴交点的知识，解答本题的关键是求出抛物线y=x2-4x+c的对称轴，此题难度不大．
练习册系列答案
相关题目
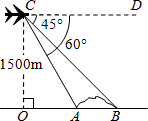如图，在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度．已知在离地面1500m高度C处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°．求油污带AB的长．（参考数据：$\sqrt{3}$=1.73）
4．下列图形中∠1与∠2互为对顶角的是（ ）
| A． |  | B． |  | C． |  | D． |  |
1．下列命题中，假命题的是（ ）
| A． | a，b，c是直线，若a∥b，b∥c，则a∥c | |
| B． | a，b，c是直线，若a⊥b，b⊥c，则a∥c | |
| C． | a，b，c是直线，若a⊥b，a⊥b，a⊥c，则b⊥c | |
| D． | a，b，c是直线，若a⊥b，b∥c，则a⊥c |
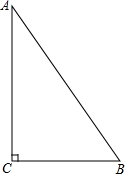（1）如图，试用直尺与圆规在平面内确定一点O，使得点O到Rt△ABC的两边AC、BC的距离相等，并且点O到A、B两点的距离也相等．（不写作法，但需保留作图痕迹）
如图，一个平行四边形的活动框架，对角线是两根橡皮筋，若改变框架的性状，则∠α也随之变化，两条对角线长度也在发生改变，当∠α是（ ）度时，两条对角线长度相等．