题目内容
4.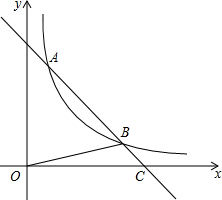 如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )
如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个,或1个,或2个 |
分析 令直线y=-x+5与y轴的交点为点D,过点B作BE⊥x轴于点E,根据一次函数图象上点的坐标特征以及△BOC的面积是$\frac{5}{2}$即可得出BE的长度,进而可找出点B的坐标,根据反比例函数图象上点的坐标特征即可得出反比例函数系数k的值,根据平移的性质找出平移后的直线的解析式将其代入反比例函数解析式中,整理后根据根的判别式的正负即可得出结论.
解答 解:令直线y=-x+5与y轴的交点为点D,过点B作BE⊥x轴于点E,如图所示.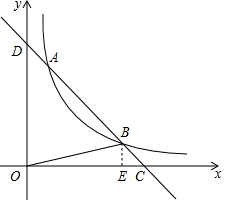
令直线y=-x+5中y=0,则0=-x+5,解得:x=5,
即OC=5.
∵△BOC的面积是$\frac{5}{2}$,
∴$\frac{1}{2}$OC•BE=$\frac{1}{2}$×5•BE=$\frac{5}{2}$,
解得:BE=1.
结合题意可知点B的纵坐标为1,
当y=1时,有1=-x+5,
解得:x=4,
∴点B的坐标为(4,1),
∴k=4×1=4,
即双曲线解析式为y=$\frac{4}{x}$.
将直线y=-x+5向下平移1个单位得到的直线的解析式为y=-x+5-1=-x+4,
将y=-x+4代入到y=$\frac{4}{x}$中,得:-x+4=$\frac{4}{x}$,
整理得:x2-4x+4=0,
∵△=(-4)2-4×4=0,
∴平移后的直线与双曲线y=$\frac{4}{x}$只有一个交点.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及三角形的面积公式,根据三角形的面积公式找出点B的坐标是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.13世纪数学家斐波那契的《计算书》中有这样一个问题:“在罗马有7位老妇人,每人赶着7头毛驴,每头驴驮着7只口袋,每只口袋里装着7个面包,每个面包附有7把餐刀,每把餐刀有7只刀鞘”,则刀鞘数为( )
| A. | 42 | B. | 49 | C. | 76 | D. | 77 |
9.已知二次函数y=ax2-bx-2(a≠0)的图象的顶点在第四象限,且过点(-1,0),当a-b为整数时,ab的值为( )
| A. | $\frac{3}{4}$或1 | B. | $\frac{1}{4}$或1 | C. | $\frac{3}{4}$或$\frac{1}{2}$ | D. | $\frac{1}{4}$或$\frac{3}{4}$ |
 如图,有一块三角形材料(△ABC),请用尺规画出△ABC的外接圆.(不写作法,保留作图痕迹)
如图,有一块三角形材料(△ABC),请用尺规画出△ABC的外接圆.(不写作法,保留作图痕迹)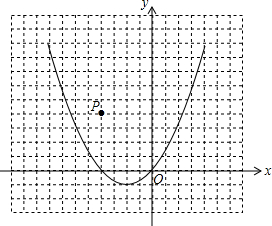 已知二次函数y=x2+x的图象,如图所示
已知二次函数y=x2+x的图象,如图所示 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是(21008,0).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是(21008,0).
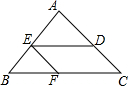 如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为13cm.
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为13cm.