题目内容
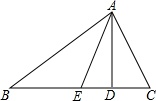 如图AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,求∠AED的度数.
如图AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,求∠AED的度数.考点:三角形内角和定理,三角形的外角性质
专题:计算题
分析:先由AD为高得到∠ADC=90°,则利用互余计算出∠CAD=90°-∠C=20°,再根据三角形内角和定理计算出∠BAC=180°-∠B-∠C=80°,接着利用角平分线定义得∠CAE=
∠BAC=40°,然后利用∠AED=∠CAE-∠CAD进行计算即可.
| 1 |
| 2 |
解答:解:∵AD为高,
∴∠ADC=90°,
∴∠CAD=90°-∠C=90°-70°=20°,
∵∠BAC=180°-∠B-∠C=180°-30°-70°=80°,
而AE为角平分线,
∴∠CAE=
∠BAC=40°,
∴∠AED=∠CAE-∠CAD=40°-20°=20°.
∴∠ADC=90°,
∴∠CAD=90°-∠C=90°-70°=20°,
∵∠BAC=180°-∠B-∠C=180°-30°-70°=80°,
而AE为角平分线,
∴∠CAE=
| 1 |
| 2 |
∴∠AED=∠CAE-∠CAD=40°-20°=20°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.

练习册系列答案
相关题目
若a<b,则下列各式不成立的是( )
| A、ac<bc | ||||
B、
| ||||
| C、a+c<b+c | ||||
| D、a-c<b-c |
下列用含字母的数字表示的数量关系中,错误的是( )
A、“a与b两数的倒数和“可表示为
| ||||
B、“与m的积是
| ||||
| C、“x的相反数与y的差的2倍“可表示为2(-x-y) | ||||
| D、“比a和b两数差的平方小3的数“可表示为(a2-b2)-3 |
(x+y+z)2=( )2+2y( )+y2,两个括号内应填( )?
| A、x+y | B、y+z |
| C、x+z | D、x+y+z |
 如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.
如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.