题目内容
已知:a=2008x+2007,b=2008x+2008,c=2008x+2009,求a2+b2+c2-ab-bc-ac的值.
考点:因式分解的应用
专题:
分析:由已知求出a-b,b-c,a-c的值,原式变形后,利用完全平方公式变形,将各自的值代入计算即可求出值.
解答:解:∵a=2008x+2007,b=2008x+2008,c=2008x+2009,
∴a-b=-1,b-c=-1,a-c=-2,
则原式=
(2a2+2b2+2c2-2ab-2bc-2ac)
=
[(a-b)2+(b-c)2+(a-c)2]
=
×(1+1+4)
=3.
故a2+b2+c2-ab-bc-ac的值是3.
∴a-b=-1,b-c=-1,a-c=-2,
则原式=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=3.
故a2+b2+c2-ab-bc-ac的值是3.
点评:此题考查了因式分解的应用,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
若a<b,则下列各式不成立的是( )
| A、ac<bc | ||||
B、
| ||||
| C、a+c<b+c | ||||
| D、a-c<b-c |
 在圆内接正方形ABCD中,AC是对角线,BE⊥AC于点E,点F为弧CD的中点,链接AF交CD于P,连接DF,则图中相似三角形有
在圆内接正方形ABCD中,AC是对角线,BE⊥AC于点E,点F为弧CD的中点,链接AF交CD于P,连接DF,则图中相似三角形有 如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.
如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.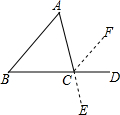 小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的作法证明出来吗?
小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的作法证明出来吗?