题目内容
现有若干个三角形，在所有的内角中，有4个直角，2个钝角，21个锐角，则在这些三角形中锐角三角形的个数是（ ）
| A、15 | B、5 | C、6 | D、3 |
考点：三角形内角和定理
专题：计算题
分析：先根据角的个数判断三角形的个数，再根据三角形内角和定理，由于有4个直角，2个钝角，则有4个直角三角形和2个钝角三角形，则余下的三角形为锐角三角形．
解答：解：共有4+2+21=27个角，则共有27÷3=9（个）三角形，
而有4个直角，2个钝角，
所以有4个直角三角形和2个钝角三角形，
所以锐角三角形的个数=9-4-2=3．
故选D．
而有4个直角，2个钝角，
所以有4个直角三角形和2个钝角三角形，
所以锐角三角形的个数=9-4-2=3．
故选D．
点评：本题考查了三角形内角和定理：三角形内角和是180°．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图，△ABC、△ACD是一副斜边相等的直角三角板，连接BD交公共的斜边AC于点O，求∠COD的度数．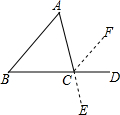
小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法，即延长BC到D，延长AC到E，过点C作CF∥AB，你能接着他的辅助线的作法证明出来吗？
如图，小东在足球场的中间位置，从A点出发，每走6m向左转60°，已知AB=BC=6m．在下列各式中，是关于x的分式方程的是（ ）
| A、2x-3y=0 | ||||
B、
| ||||
C、
| ||||
D、
|
下列说法错误的是（ ）
| A、两个等边三角形一定相似 |
| B、两个正方形一定相似 |
| C、两个菱形一定相似 |
| D、两个全等三角形一定相似 |