题目内容
12.函数y=$\frac{\sqrt{7-2x}}{x-2}$的自变量x的取值范围是x≤$\frac{7}{2}$且x≠2.分析 根据分式和二次根式有意义的条件得出7-2x≥0且x-2≠0,解不等式组即可.
解答 解:∵7-2x≥0且x-2≠0,
∴x≤$\frac{7}{2}$且x≠2,
故答案为x≤$\frac{7}{2}$且x≠2.
点评 本题考查了函数自变量的取值范围问题,熟记分式有意义的条件:分母不为0和二次根式有意义的条件是被开方数大于等于0是解题的关键.

练习册系列答案
相关题目
7.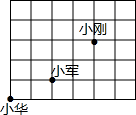 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )| A. | (1,2) | B. | (1,3) | C. | (0,2) | D. | (2,2) |
17.探究多边形内角和公式时,从n边形的一个顶点出发引出(n-3)条对角线,将n边形分割成(n-2)个三角形,这(n-2)个三角形的所有内角之和即为n边形的内角和,这一探究过程运用的数学思想是( )
| A. | 方程思想 | B. | 函数思想 | C. | 数形结合思想 | D. | 化归思想 |
4.直线l是以二元一次方程8x-4y=5的解为坐标所构成的直线,则该直线不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.下列命题中,为真命题的是( )
| A. | 六边形的内角和为360度 | B. | 多边形的外角和与边数有关 | ||
| C. | 面积相等的三角形全等 | D. | 三角形两边的和大于第三边 |
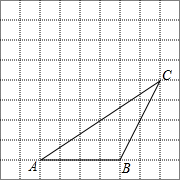 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.