题目内容
4.一元二次方程x2-3x+1=0与x2-x+3=0的所有实数根的和等于3.分析 先根据一元二次方程的根的判别式可得到一元二次方程x2-3x+1=0有两个不相等的实数根,x2-3x+3=0没有实数根,再根据一元二次方程的根与系数的关系得到一元二次方程x2-3x+1=0两根之和=-(-3)=3,即可得到一元二次方程x2-3x-1=0与x2-3x+3=0的所有实数根的和.
解答 解:∵一元二次方程x2-3x=1=0的判别式△=(-3)2-4×1×1=5>0,
∴一元二次方程x2-3x+1=0有两个不相等的实数根,
∴两根之和=-(-3)=3,
又∵x2-3x+3=0的判别式△=(-3)2-4×1×3=-3<0,
∴x2-3x+3=0没有实数根,
∴一元二次方程x2-3x-1=0与x2-3x+3=0的所有实数根的和等于3.
故答案为:3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了一元二次方程的根的判别式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.某商场销售同型号A,B两种品牌的节能灯管,它们进价相同,A品牌售价可变,最低售价不能低于进价,最高利润不超过4元.B品牌售价不变,它们每只的销售利润与梅州销售量的关系如表(售价=进价+利润)
(1)当A品牌每周的销售量为300只时,B品牌每周的销售量为多少只?
(2)A品牌的售价对B品牌的销售量有什么影响?
(3)A品牌节能灯管每只利润定为多少元时,可获得最大总利润?并求出最大总利润.
| 品牌 | 每只销售利润/元 | 每周销售量/只 |
| A | x | -300x+1200 |
| B | 2 | 当0<x<3时,120x+140 当3≤x≤4时,500 |
(2)A品牌的售价对B品牌的销售量有什么影响?
(3)A品牌节能灯管每只利润定为多少元时,可获得最大总利润?并求出最大总利润.
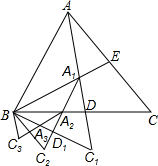 已知如图,△ABC是面积为1的正三角形,AC和BC两边上的高BE与AD相交于点A1,延长AD到C1,使C1D=A1D,连接BC1,得△A1BC1,作其BC1边上的高A1D1交BD于A2,延长A1D1到C2,使A2D1=C2D1,连接BC2,得△A2BC2,有同样的方法得△A3BC3…当AnB与AB第一次重合时,△AnBCn的面积是$\frac{1}{{3}^{12}}$.
已知如图,△ABC是面积为1的正三角形,AC和BC两边上的高BE与AD相交于点A1,延长AD到C1,使C1D=A1D,连接BC1,得△A1BC1,作其BC1边上的高A1D1交BD于A2,延长A1D1到C2,使A2D1=C2D1,连接BC2,得△A2BC2,有同样的方法得△A3BC3…当AnB与AB第一次重合时,△AnBCn的面积是$\frac{1}{{3}^{12}}$.
 y与x的函数图象如图所示,当0≤x≤100时,y与x的函数关系式为y=100x;当x>100时,y与x的函数关系式为y=60x+4000.
y与x的函数图象如图所示,当0≤x≤100时,y与x的函数关系式为y=100x;当x>100时,y与x的函数关系式为y=60x+4000.
 如图:AB=CD,AE=DF,CE=FB.求证:AE∥DF.
如图:AB=CD,AE=DF,CE=FB.求证:AE∥DF.