题目内容
12.已知关于x,y的方程组$\left\{\begin{array}{l}{y-ax+4=0}\\{y=x-b}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$.(1)在同一直角坐标系内画出这两个方程确定的函数图象.
(2)分别求出它们与x轴的交点A、B的坐标;
(3)设两图象的交点为C,求△ABC的面积.
分析 (1)把x,y的值代入方程组,即可得出a,b的值,再根据一次函数图象的画法画出图象即可;
(2)分别令y=0,即可得出点A,B的横坐标,进而得出A、B的坐标;
(3)根据交点的意义可得出点C坐标(2,4),再根据三角形的面积公式求解即可.
解答 解:(1)把$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{y-ax+4=0}\\{y=x-b}\end{array}\right.$,得$\left\{\begin{array}{l}{a=4}\\{b=-2}\end{array}\right.$,
∴两个函数的解析式为:y=4x-4,y=x+2,
画图象如图:
(2)令y=0,得4x-4=0,x+2=0,
解得x=1,x=-2,
得出点A(1,0),B(-2,0);
(3)∵两图象的交点为C,
∴C(2,4),
∵AB=3,
∴S△ABC=$\frac{1}{2}$AB•yC=$\frac{1}{2}$×3×4=6.
点评 本题考查了二元一次方程组的解,以及一次函数的图象的画法,三角形面积的求法,是一道综合题,难度不大.

练习册系列答案
相关题目
 如图,∠1=∠2,∠B=∠D,求证:AB=CD.
如图,∠1=∠2,∠B=∠D,求证:AB=CD.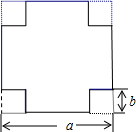 如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米?
如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米?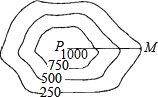 测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732)
测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732)