题目内容
16.某商场销售同型号A,B两种品牌的节能灯管,它们进价相同,A品牌售价可变,最低售价不能低于进价,最高利润不超过4元.B品牌售价不变,它们每只的销售利润与梅州销售量的关系如表(售价=进价+利润)| 品牌 | 每只销售利润/元 | 每周销售量/只 |
| A | x | -300x+1200 |
| B | 2 | 当0<x<3时,120x+140 当3≤x≤4时,500 |
(2)A品牌的售价对B品牌的销售量有什么影响?
(3)A品牌节能灯管每只利润定为多少元时,可获得最大总利润?并求出最大总利润.
分析 (1)当A品牌每周的销售量为300只时,即-300x+1200=300,解得:x=3,确定x的范围,即可解答;
(2)根据当0<x<3时,B每周销售量为:120x+140;当3≤x≤4时,B每周销售量500,当A品牌的售价高时,对B品牌的销售量更能起促进作用;当A品牌的售价低时,对B品牌的销售量更能起反作用.
(3)设A品牌每周销售总利润为y元,则y=x(-300x+1200)=-300x2+1200x=-300(x-2)2+1200,根据二次函数的性质,即可解答.
解答 解:(1)当A品牌每周的销售量为300只时,即-300x+1200=300,
解得:x=3,
由B每周销售量可知:当3≤x≤4时,B品牌每周的销售量为500只.
(2)∵当0<x<3时,B每周销售量为:120x+140;当3≤x≤4时,B每周销售量500
当A品牌的售价高时,对B品牌的销售量更能起促进作用;当A品牌的售价低时,对B品牌的销售量更能起反作用.
(3)设A品牌每周销售总利润为y元,
则y=x(-300x+1200)=-300x2+1200x=-300(x-2)2+1200,
∵-300<0,
∴当x=2时,可以获得最大总利润,最大总利润为1200元.
点评 本题考查二次函数的应用,根据二次函数的对称轴得到离抛物线的对称轴最近的数是可获得最大利润的销售量是解决本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
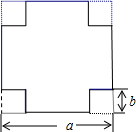 如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米?
如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米?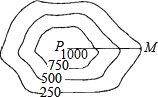 测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732)
测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732) 如图,△ABC中,∠1=∠2,∠3=∠4,EF∥BC,说明BE+CF=EF.
如图,△ABC中,∠1=∠2,∠3=∠4,EF∥BC,说明BE+CF=EF.