题目内容
14.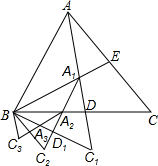 已知如图,△ABC是面积为1的正三角形,AC和BC两边上的高BE与AD相交于点A1,延长AD到C1,使C1D=A1D,连接BC1,得△A1BC1,作其BC1边上的高A1D1交BD于A2,延长A1D1到C2,使A2D1=C2D1,连接BC2,得△A2BC2,有同样的方法得△A3BC3…当AnB与AB第一次重合时,△AnBCn的面积是$\frac{1}{{3}^{12}}$.
已知如图,△ABC是面积为1的正三角形,AC和BC两边上的高BE与AD相交于点A1,延长AD到C1,使C1D=A1D,连接BC1,得△A1BC1,作其BC1边上的高A1D1交BD于A2,延长A1D1到C2,使A2D1=C2D1,连接BC2,得△A2BC2,有同样的方法得△A3BC3…当AnB与AB第一次重合时,△AnBCn的面积是$\frac{1}{{3}^{12}}$.
分析 根据△ABC是面积为1的正三角形,得出△A1BC1的面积为$\frac{1}{3}$,进而得出△A2BC2的面积为$\frac{1}{9}$,以此类推解答即可.
解答 解:∵△ABC是面积为1的正三角形,AC和BC两边上的高BE与AD相交于点A1,
∴△ABD的面积为$\frac{1}{2}$,
∴△A1BD的面积为$\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$,
∵延长AD到C1,使C1D=A1D,连接BC1,得△A1BC1,
∴△A1BC1的面积为$2×\frac{1}{6}=\frac{1}{3}$,
同理可得:△A2BC2的面积为$\frac{1}{9}$,
以此类推可得:△AnBCn的面积是$\frac{1}{{3}^{12}}$,
故答案为:$\frac{1}{{3}^{12}}$.
点评 此题考查正三角形的性质,关键是得出△A1BC1的面积为$\frac{1}{3}$和△A2BC2的面积为$\frac{1}{9}$,根据规律解答即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.2015年某企业有4000名职工,为了了解职工本年度第一季度网上购物的情况,该企业从中随机抽取了350名职工,按年龄分布和对网上购物情况进行了调查统计,并将统计结果绘成了频数分布直方图(每个组距包含左边的数,但不包含右边的数)和扇形图.
(1)这次调查中,如果被调查职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
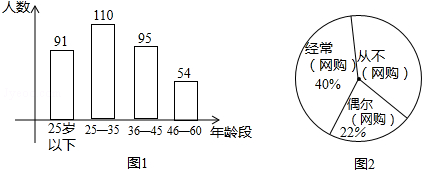
(2)你估计这个企业的4000名职工中,从不网购的有多少人?
(3)统计显示,买同样的商品,经常网购的人比在一般商店购买能节省20%,偶尔网购的人比在一般商店购买能节省15%,样本中,职工第一季度网购商品共消费24500元,这些商品若在一般商店购买需要30000元,请问,经常网购的一组和偶尔网购的一组本季度网购商品各消费多少元?
(4)如果在样本中,本季度网购情况如下表:
请你计算该样本中,本季度进行网购的人平均每人网上购物几次?
(1)这次调查中,如果被调查职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?

(2)你估计这个企业的4000名职工中,从不网购的有多少人?
(3)统计显示,买同样的商品,经常网购的人比在一般商店购买能节省20%,偶尔网购的人比在一般商店购买能节省15%,样本中,职工第一季度网购商品共消费24500元,这些商品若在一般商店购买需要30000元,请问,经常网购的一组和偶尔网购的一组本季度网购商品各消费多少元?
(4)如果在样本中,本季度网购情况如下表:
| 网购次数/次 | 1 | 2 | 3 | 4 | 5 |
| 人数/人 | 37 | 40 | 63 | 40 | 37 |
19.为了了解某种型号的电风扇的使用寿命,从中抽取30台进行测试,在这个问题中,30台电风扇的使用寿命是( )
| A. | 总体 | B. | 个体 | C. | 样本 | D. | 样本容量 |
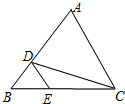 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△BAC=1:9,则 S△BDE:S△CDE=1:2.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△BAC=1:9,则 S△BDE:S△CDE=1:2. 如图,∠1=∠2,∠B=∠D,求证:AB=CD.
如图,∠1=∠2,∠B=∠D,求证:AB=CD.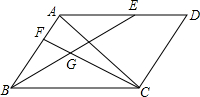 如图,平行四边形ABCD中,AB=5,AD=7,AB⊥AC,点E在边AD上,满足$\frac{AE}{AD}$=$\frac{2}{3}$,点F在AB上,满足$\frac{AF}{AB}$=$\frac{2}{5}$,连结BE和CF相交于点G,则线段CG的长度是$\frac{10\sqrt{7}}{7}$.
如图,平行四边形ABCD中,AB=5,AD=7,AB⊥AC,点E在边AD上,满足$\frac{AE}{AD}$=$\frac{2}{3}$,点F在AB上,满足$\frac{AF}{AB}$=$\frac{2}{5}$,连结BE和CF相交于点G,则线段CG的长度是$\frac{10\sqrt{7}}{7}$.