题目内容
5.已知长方形纸带,∠DEF=20°,将纸带沿EF折叠成图案②,则图②中的∠EGB的度数是40°.
分析 根据折叠求出∠FEG=∠DEF=20°,根据平行线的性质求出即可.
解答 解:∵∠DEF=20°,将纸带沿EF折叠成图案②,
∴∠FEG=∠DEF=20°,
∵AD∥BC,
∴∠EGB=20°+20°=40°,
故答案为:40°.
点评 本题考查了平行线的性质,折叠的性质的应用,能求出∠FEG=∠DEF=20°和求出∠EGB=20°+20°是解此题的关键,注意:两直线平行,内错角相等.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
16.下列各式中与$\sqrt{6}$是同类二次根式的是( )
| A. | $\root{3}{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
13.若把分式$\frac{x+3y}{2x}$的x、y同时缩小12倍,则分式的值( )
| A. | 不变 | B. | 缩小12倍 | C. | 扩大12倍 | D. | 缩小6倍 |
10.若不等式组$\left\{\begin{array}{l}{x>2}\\{x>m}\end{array}\right.$的解集是x>2,则m的取值范围是( )
| A. | m>2 | B. | m≥2 | C. | m<2 | D. | m≤2 |
17.下列各组数中互为相反数的是( )
| A. | |-2|与2 | B. | -2与$\root{3}{-8}$ | C. | -2与$-\frac{1}{2}$ | D. | -2与$\sqrt{{{(-2)}^2}}$ |
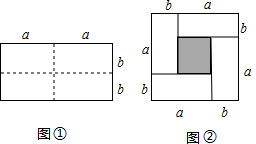 图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.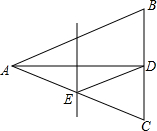 如图,△ABC中,AB=AC=13,BC=10,AD平分∠BAC交BC于点D,AD的垂直平分线交AC于点E,连接DE,则△CDE的周长为18.
如图,△ABC中,AB=AC=13,BC=10,AD平分∠BAC交BC于点D,AD的垂直平分线交AC于点E,连接DE,则△CDE的周长为18.