题目内容
18.计算:(1)$\sqrt{3}$($\sqrt{6}$+5$\sqrt{8}$)
(2)(2$\sqrt{3}$+3$\sqrt{2}$)(2$\sqrt{3}$-3$\sqrt{2}$)
(3)(5$\sqrt{2}$+$\sqrt{5}$)2.
(4)($\sqrt{48}$+$\frac{1}{4}\sqrt{6}$)÷$\sqrt{3}$.
分析 (1)利用二次根式的乘法法则运算;
(2)利用平方差公式计算;
(3)利用完全平方公式计算;
(4)利用二次根式的除法法则运算.
解答 解:(1)原式=$\sqrt{3×6}$+5$\sqrt{3×8}$
=3$\sqrt{2}$+10$\sqrt{6}$;
(2)原式=12-18
=-6;
(3)原式=50+10$\sqrt{10}$+5
=55+10$\sqrt{10}$;
(4)原式=$\sqrt{48÷3}$+$\frac{1}{4}$$\sqrt{6÷3}$
=4+$\frac{\sqrt{2}}{4}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 已知函数y=-x+4,回答下列问题:
已知函数y=-x+4,回答下列问题:
(1)请在右图的直角坐标系中画出函数y=-x+4图象;
(2)y的值随x值的增大而减小;
(3)当y=2时,x的值为x=2;
(4)当y<0时,x的取值范围是x>4.
 已知函数y=-x+4,回答下列问题:
已知函数y=-x+4,回答下列问题:(1)请在右图的直角坐标系中画出函数y=-x+4图象;
(2)y的值随x值的增大而减小;
(3)当y=2时,x的值为x=2;
(4)当y<0时,x的取值范围是x>4.
6.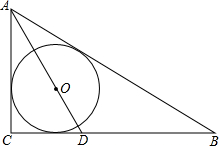 如图,在Rt△ABC中,∠ACB=90°,周长为20,⊙O为△ABC内切圆,连接AO交BC于点D,且CD:BD=2:3,则△ABC内切圆的半径为( )
如图,在Rt△ABC中,∠ACB=90°,周长为20,⊙O为△ABC内切圆,连接AO交BC于点D,且CD:BD=2:3,则△ABC内切圆的半径为( )
 如图,在Rt△ABC中,∠ACB=90°,周长为20,⊙O为△ABC内切圆,连接AO交BC于点D,且CD:BD=2:3,则△ABC内切圆的半径为( )
如图,在Rt△ABC中,∠ACB=90°,周长为20,⊙O为△ABC内切圆,连接AO交BC于点D,且CD:BD=2:3,则△ABC内切圆的半径为( )| A. | $\sqrt{5}$-1 | B. | $\sqrt{5}$+1 | C. | 3$\sqrt{5}$-5 | D. | 6$\sqrt{5}$-10 |
7.在样本容量为160的频数直方图中,共有3个小长方形,若中间一个小长方形的高与其余两个小长方形高的和之比是2:3,则中间一组的频率为( )
| A. | 0.2 | B. | 0.25 | C. | 0.4 | D. | 0.6 |
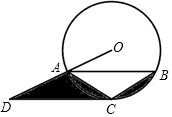 如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.
如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.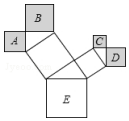 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、E的面积分别为2,5,1,10.则正方形D的面积是2.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、E的面积分别为2,5,1,10.则正方形D的面积是2. ,则阴影部分图形的面积为( )
,则阴影部分图形的面积为( )
 B.
B.  C.
C.  D.
D. 