题目内容
同一圆的内接正三角形、正方形,正五边形,正六边形中,周长最大的是 .
考点:正多边形和圆
专题:
分析:首先根据题意画出图形,根据正多边形的性质易得AB=2AM=2OA•cos∠AOM,然后求得圆的内接正三角形、正方形,正五边形,正六边形的圆心角分别为:120°,90°,72°,60°,又由余弦的增减性,求得答案.
解答: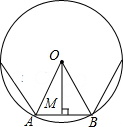 解:如图,是正多边形的一部分,过点O作OM⊥AB于点M,
解:如图,是正多边形的一部分,过点O作OM⊥AB于点M,
∵OA=OB,
∴AM=
AB,∠AOM=
AOB,
即AB=2AM=2OA•cos∠AOM,
∵圆的内接正三角形、正方形,正五边形,正六边形的圆心角分别为:120°,90°,72°,60°,
∴内接正三角形、正方形,正五边形,正六边形对应的∠AOM分别为:60°,45°,36°,30°,
∵cos∠AOM随着∠AOM的增大而减小,
∴正六边形的边长最大,
∴周长最大的是正六边形.
故答案为:正六边形.
 解:如图,是正多边形的一部分,过点O作OM⊥AB于点M,
解:如图,是正多边形的一部分,过点O作OM⊥AB于点M,∵OA=OB,
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
即AB=2AM=2OA•cos∠AOM,
∵圆的内接正三角形、正方形,正五边形,正六边形的圆心角分别为:120°,90°,72°,60°,
∴内接正三角形、正方形,正五边形,正六边形对应的∠AOM分别为:60°,45°,36°,30°,
∵cos∠AOM随着∠AOM的增大而减小,
∴正六边形的边长最大,
∴周长最大的是正六边形.
故答案为:正六边形.
点评:此题考查了正多边形与圆的知识.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
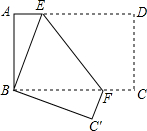 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′出,折痕为EF,
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′出,折痕为EF, 把下面的直线补充成一条数轴,然后在数轴上标出下列各数,并按从小到大的顺序用“<“连接起来.
把下面的直线补充成一条数轴,然后在数轴上标出下列各数,并按从小到大的顺序用“<“连接起来. 如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.求证:△OEF是等腰三角形.
如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.求证:△OEF是等腰三角形. 如图,有甲、乙两建筑物,甲建筑物的高度为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.
如图,有甲、乙两建筑物,甲建筑物的高度为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.