题目内容
若AB是⊙O内接正五边形的一边,AC是⊙O的内接正六边形的一边,则∠BAC等于 .
考点:正多边形和圆
专题:
分析:先根据题意画出图形,根据正多边形与圆的关系分别求出中心角∠AOC=60°,∠AOB=72°,再由等边对等角及三角形内角和定理分别求出∠OAC=54°,∠OAB=54°,然后分两种情况进行讨论:①AB、AC都在OA同侧;②AB、AC在OA两侧.
解答: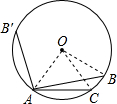 解:如图,连接OA,OB,OC,
解:如图,连接OA,OB,OC,
∵AB是⊙O内接正五边形的一边,AC是⊙O的内接正六边形的一边,
∴∠AOC=
=60°,∠AOB=
=72°,
∵OA=OC=OB,
∴∠OAB=54°,∠OAC=60°,
若AB与AC在OA的同侧,∠BAC=∠OAC-∠OAB=6°,
当AB、AC在OA两侧时,则∠BAC=∠OAC+∠OAB=54°+60°=114°.
∴∠BAC=6°或114°.
故答案为:6°或114°.
 解:如图,连接OA,OB,OC,
解:如图,连接OA,OB,OC,∵AB是⊙O内接正五边形的一边,AC是⊙O的内接正六边形的一边,
∴∠AOC=
| 360° |
| 6 |
| 360° |
| 5 |
∵OA=OC=OB,
∴∠OAB=54°,∠OAC=60°,
若AB与AC在OA的同侧,∠BAC=∠OAC-∠OAB=6°,
当AB、AC在OA两侧时,则∠BAC=∠OAC+∠OAB=54°+60°=114°.
∴∠BAC=6°或114°.
故答案为:6°或114°.
点评:本题考查了正多边形与圆的关系,等边对等角及三角形内角和定理,正确画出图形,进行分类讨论是解题的关键.

练习册系列答案
相关题目
经过平面上4个点中的每两个点画直线,最多可以画( )
| A、2条 | B、6条 | C、4条 | D、3条 |
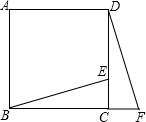 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,BE与DF之间有怎样的关系?说明理由.
如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,BE与DF之间有怎样的关系?说明理由.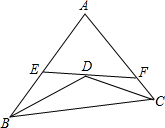 如图,BD,CD分别平分∠ABC,∠ACB,过点D作直线分别交AB,AC于点E,F,若AE=AF,BE=4,CF=2,则EF的长为( )
如图,BD,CD分别平分∠ABC,∠ACB,过点D作直线分别交AB,AC于点E,F,若AE=AF,BE=4,CF=2,则EF的长为( )
 如图所示,在河a两岸有A、B两个村庄,现在要在河上修建一座大桥,为方便交通,要使桥到这两村庄的距离之和最短,应在河上哪一点修建才能满足要求?(画出图形,做出说明.)
如图所示,在河a两岸有A、B两个村庄,现在要在河上修建一座大桥,为方便交通,要使桥到这两村庄的距离之和最短,应在河上哪一点修建才能满足要求?(画出图形,做出说明.)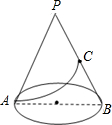 如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.
如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.