题目内容
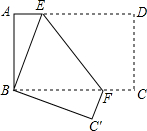 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′出,折痕为EF,
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′出,折痕为EF,(1)求证:BE=BF.
(2)若∠ABE=20°,求∠BFE的度数.
(3)若AB=6,AD=8,求AE的长.
考点:翻折变换(折叠问题)
专题:
分析:(1)根据翻折变换的性质,结合矩形的性质证明∠BEF=∠BFE即可解决问题.
(2)根据矩形的性质及等腰三角形的性质即可解决问题.
(3)根据勾股定理列出关于线段AE的方程即可解决问题.
(2)根据矩形的性质及等腰三角形的性质即可解决问题.
(3)根据勾股定理列出关于线段AE的方程即可解决问题.
解答: 解:(1)由题意得:∠BEF=∠DEF;
解:(1)由题意得:∠BEF=∠DEF;
∵四边形ABCD为矩形,
∴DE∥BF,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF.
(2)∵四边形ABCD为矩形,
∴∠ABF=90°;而∠ABE=30°,
∴∠EBF=90°-30°=60°;
又∵BE=BF,
∴△BEF为等边三角形,
∴∠BFE的度数为60°.
(3)由题意知:BE=DE;
设AE=x,则BE=DE=8-x,
由勾股定理得:
(8-x)2=62+x2,
解得:x=
.
即AE的长为
.
 解:(1)由题意得:∠BEF=∠DEF;
解:(1)由题意得:∠BEF=∠DEF;∵四边形ABCD为矩形,
∴DE∥BF,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF.
(2)∵四边形ABCD为矩形,
∴∠ABF=90°;而∠ABE=30°,
∴∠EBF=90°-30°=60°;
又∵BE=BF,
∴△BEF为等边三角形,
∴∠BFE的度数为60°.
(3)由题意知:BE=DE;
设AE=x,则BE=DE=8-x,
由勾股定理得:
(8-x)2=62+x2,
解得:x=
| 7 |
| 4 |
即AE的长为
| 7 |
| 4 |
点评:该命题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用全等三角形的性质、勾股定理等几何知识点来解题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
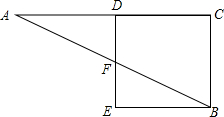 如图,在△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,DF=2,AF=BF,则四边形BCDE的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,DF=2,AF=BF,则四边形BCDE的周长为( )A、4
| ||
| B、8 | ||
C、4+4
| ||
D、8+4
|
已知等腰三角形的一边长为6,一个内角为60°,则它的周长是( )
| A、12 | B、15 | C、16 | D、18 |
 如图,AD是△ABC的BC边上的中线,AB=7,AD=5,则AC的取值范围为
如图,AD是△ABC的BC边上的中线,AB=7,AD=5,则AC的取值范围为 如图所示,在河a两岸有A、B两个村庄,现在要在河上修建一座大桥,为方便交通,要使桥到这两村庄的距离之和最短,应在河上哪一点修建才能满足要求?(画出图形,做出说明.)
如图所示,在河a两岸有A、B两个村庄,现在要在河上修建一座大桥,为方便交通,要使桥到这两村庄的距离之和最短,应在河上哪一点修建才能满足要求?(画出图形,做出说明.)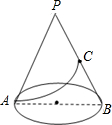 如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.
如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.