题目内容
已知∠A的两边与∠B的两边分别互相垂直,若∠A=80°,则∠B= .
考点:垂线
专题:分类讨论
分析:根据垂直的定义,可得∠C、∠D的度数,根据四边形的内角和,可得答案.
解答:解:如图:
 ,
,
∵BC⊥AC,BD⊥AD,
∴∠C=∠D=90°.
由四边形的内角和,得
∠A+∠B+∠C+∠D=(4-2)×180°=360°,
即∠B=360°-∠A-∠C-∠D=360°-80°-90°-90°=100°,
故答案为:100°.
 ,
,∵BC⊥AC,BD⊥AD,
∴∠C=∠D=90°.
由四边形的内角和,得
∠A+∠B+∠C+∠D=(4-2)×180°=360°,
即∠B=360°-∠A-∠C-∠D=360°-80°-90°-90°=100°,
故答案为:100°.
点评:本题考查了垂线,利用了垂线的定义,四边形内角和公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
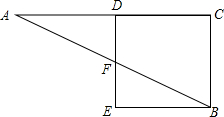 如图,在△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,DF=2,AF=BF,则四边形BCDE的周长为( )
如图,在△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,DF=2,AF=BF,则四边形BCDE的周长为( )A、4
| ||
| B、8 | ||
C、4+4
| ||
D、8+4
|
经过平面上4个点中的每两个点画直线,最多可以画( )
| A、2条 | B、6条 | C、4条 | D、3条 |
已知等腰三角形的一边长为6,一个内角为60°,则它的周长是( )
| A、12 | B、15 | C、16 | D、18 |
 如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )
如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )A、
| ||||
B、
| ||||
| C、∠ABP=∠C | ||||
| D、∠APB=∠ABC |
 如图是拉线固定电线杆的示意图.点A、D、B在同一直线上.已知CD⊥AB,CD=3
如图是拉线固定电线杆的示意图.点A、D、B在同一直线上.已知CD⊥AB,CD=3