题目内容
4.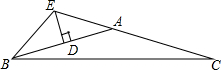 如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )
如图,△ABC中,AB=AC,AB的垂直平分线交AB于点D,交CA的延长线于点E,∠EBC=42°,则∠BAC=( )| A. | 159° | B. | 154° | C. | 152° | D. | 138° |
分析 根据等腰三角形的性质得到∠ABC=∠C,由三角形外角的性质得到∠EAB=2∠ABC,根据线段垂直平分线的性质得到∠EBA=∠EAB=2∠ABC,得到∠ABC=14°,根据三角形的内角和即可得到结论.
解答 解:∵AB=AC,
∴∠ABC=∠C,
∵∠EAB=∠ABC+∠C,
∴∠EAB=2∠ABC,
∵DE垂直平分AB,
∴∠EBA=∠EAB=2∠ABC,
∴∠EBC=3∠ABC=42°,
∴∠ABC=14°,
∴∠BAC=180°-2∠ABC=152°,
故选C.
点评 此题考查了线段垂直平分线的性质与等边三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
14.下列命题中,真命题的个数有( )
①如果直线a∥b,b∥c,那么a∥c;②相等的角是对顶角;③两条直线被第三条直线所截,同位角相等;④比正实数小的一定是负实数;⑤两条直线平行,同旁内角相等;⑥立方根等于它本身的数是-1,0,1.
①如果直线a∥b,b∥c,那么a∥c;②相等的角是对顶角;③两条直线被第三条直线所截,同位角相等;④比正实数小的一定是负实数;⑤两条直线平行,同旁内角相等;⑥立方根等于它本身的数是-1,0,1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15. 若∠1与∠2互补,∠3=130°,则∠4等于( )
若∠1与∠2互补,∠3=130°,则∠4等于( )
 若∠1与∠2互补,∠3=130°,则∠4等于( )
若∠1与∠2互补,∠3=130°,则∠4等于( )| A. | 75° | B. | 50° | C. | 45≤ | D. | 135° |
12. 如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
 如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )
如图,a∥b,直线AB分别交a、b于A、B两点,点C在直线b上,且∠1=∠2,则下列结论正确的是( )| A. | ∠1=∠ABC | B. | ∠1=∠ACB | C. | ∠ABC=∠ACB | D. | ∠2=∠ABC |
19.以下列所给线段长为三边,能构成三角形的是( )
| A. | 1cm、2cm、3cm | B. | 3cm、4cm、6cm | C. | 1cm、1cm、3cm | D. | 2cm、3cm、7cm |
9.如图,一个长方形是另一个长方形按顺时针方向旋转90°后形成的是( )


| A. | ①② | B. | ②④ | C. | ②③ | D. | ③④ |
16.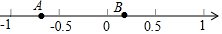 如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
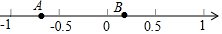 如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )| A. | 甲、乙 | B. | 甲、丙 | C. | 丙、丁 | D. | 乙、丁 |
13.下列数学符号中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
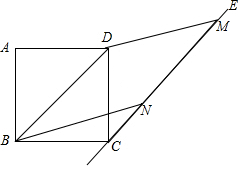 已知正方形ABCD中,过点C作直线CE,使CE∥BD;以BD为一边作?BDMN,且顶点M,N均在直线CE上,给出下列结论:
已知正方形ABCD中,过点C作直线CE,使CE∥BD;以BD为一边作?BDMN,且顶点M,N均在直线CE上,给出下列结论: