题目内容
16.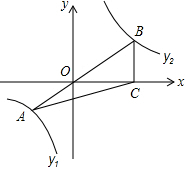 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
分析 设A(m,$\frac{4}{m}$)(m<0),则可得到直线AB的解析式为y=$\frac{4}{{m}^{2}}$x.再利用反比例函数与一次函数的交点问题可表示出B(-$\frac{1}{2}$mk,-$\frac{2k}{m}$),则利用三角形面积公式得到$\frac{1}{2}$×(-$\frac{2k}{m}$)×(-$\frac{1}{2}$mk+|m|)=$\frac{15}{2}$,解得k1=-5(舍去),k2=3,于是得到y2=$\frac{9}{x}$.
解答 解:设A(m,$\frac{4}{m}$)(m<0),
直线AB的解析式为y=ax(k≠0),
∵A(m,$\frac{4}{m}$),
∴ma=$\frac{4}{m}$,解得a=$\frac{4}{{m}^{2}}$,
∴直线AB的解析式为y=$\frac{4}{{m}^{2}}$x.
∵AO的延长线交函数y=$\frac{{k}^{2}}{x}$的图象于点B,
∴B(-$\frac{1}{2}$mk,-$\frac{2k}{m}$),
∵△ABC的面积等于$\frac{15}{2}$,CB⊥x轴,
∴$\frac{1}{2}$×(-$\frac{2k}{m}$)×(-$\frac{1}{2}$mk+|m|)=$\frac{15}{2}$,解得k1=-5(舍去),k2=3,
∴y2=$\frac{9}{x}$.
点评 本题考查了比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
6.应用题
老张装修完新房,元旦期间又到苏宁电器购买冰箱、电视机和洗衣机三件家电,刚好该商场推出新年优惠活动,具体优惠情况如下表:
比如:买原价5000元的商品,实际花费3000+(5000-3000)(1-5%)-160=4740(元)
(1)已知老张购买的这三件家电原价合计为11500元,如果一次性支付,请求出他的实际花费;
(2)如果在该商场购买一件原价为x元的商品(x≤10000),请用含x的代数式表示实际花费;
(3)付款时,老张突然想到:如果一次性支付,虽然优惠率更高,却只能享受一次立减160元优惠,如果将这三件家电分开支付或者两件合并支付,另一件单独支付,就可以享受多次立减160元优惠,这样是否可能更加划算呢?已知老张购买的冰箱原价4800元,电视机原价4600元,洗衣机原价2100元,请你通过计算帮老张设计出最优惠的支付方案.
老张装修完新房,元旦期间又到苏宁电器购买冰箱、电视机和洗衣机三件家电,刚好该商场推出新年优惠活动,具体优惠情况如下表:
| 购物金额(原价) | 优惠率 |
| 不超过3000元的部分 | 无优惠 |
| 超过3000元但不超过10000元部分 | 5% |
| 超过10000元的部分 | 10% |
| 付款时,还可以享受单笔消费满2000元立减160元优惠 | |
(1)已知老张购买的这三件家电原价合计为11500元,如果一次性支付,请求出他的实际花费;
(2)如果在该商场购买一件原价为x元的商品(x≤10000),请用含x的代数式表示实际花费;
(3)付款时,老张突然想到:如果一次性支付,虽然优惠率更高,却只能享受一次立减160元优惠,如果将这三件家电分开支付或者两件合并支付,另一件单独支付,就可以享受多次立减160元优惠,这样是否可能更加划算呢?已知老张购买的冰箱原价4800元,电视机原价4600元,洗衣机原价2100元,请你通过计算帮老张设计出最优惠的支付方案.
5. 如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )
如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )
 如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )
如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )| A. | -4 | B. | 6 | C. | 8 | D. | 12 |
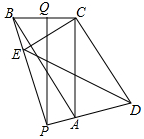 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求: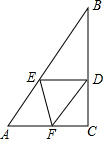 如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm. 如图,用方向和距离表示火车站相对于仓库的位置是东偏北20°方向,距离仓库50km.
如图,用方向和距离表示火车站相对于仓库的位置是东偏北20°方向,距离仓库50km.
 如图,四边形ABCD中,∠A=90°,AB=2$\sqrt{5}$,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别是DM,MN的中点,则EF长度的最大值为$\sqrt{6}$.
如图,四边形ABCD中,∠A=90°,AB=2$\sqrt{5}$,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别是DM,MN的中点,则EF长度的最大值为$\sqrt{6}$.