题目内容
4.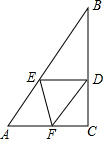 如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
分析 如图,作点D关于直线AC的对称点H,连接EH交AC于F,此时FE+FD的值最小,即△DEF的周长最小.求出DE、EH的长即可解决问题.
解答 解:如图,作点D关于直线AC的对称点H,连接EH交AC于F,此时FE+FD的值最小,即△DEF的周长最小.
在Rt△BED中,∵∠EDB=90°,∠B=30°,BE=6cm,
∴DE=3cm<BD=3$\sqrt{3}$cm,
∵BD=2CD,
∴CD=CH=$\frac{3\sqrt{3}}{2}$,
在Rt△EDH中,EH=$\sqrt{D{E}^{2}+D{H}^{2}}$=6cm,
∵FD=FH,
∴△DEF的周长的最小值=DE+EF+DF=DE+EF+FH=EH+DE=6+3=9cm,
故答案为9.
点评 本题考查轴对称-最短问题、勾股定理等知识,解题的关键是学会利用对称解决最短问题,属于中考常考题型.

练习册系列答案
相关题目
19.下列运算错误的是( )
| A. | -|-2|=2 | B. | (6.4×106)÷(8×103)=800 | ||
| C. | (-1)2015-12016=-2 | D. | $-6÷({\frac{1}{3}-\frac{1}{2}})=36$ |
14.将抛物线y=-x2向左移动2个单位,再向上移动3个单位后,抛物线的顶点为( )
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
 在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).
在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).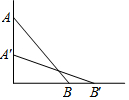 如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.
如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.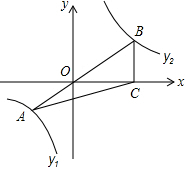 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2. 已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.
已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.