题目内容
△ABC中,D、E、F分别是在AB、AC、BC上的点,DE∥BC,EF∥AB,那么下列各式正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平行线分线段成比例
专题:
分析:根据平行线分线段成比例定理,由DE∥BC得到
=
,则可对以D进行判断;再由EF∥AB得
=
,则
=
,于是可对A、C进行判断;由EF∥AB得
=
,利用比例的性质可对B进行判断.
| AD |
| DB |
| AE |
| EC |
| AE |
| EC |
| BF |
| FC |
| AD |
| DB |
| BF |
| FC |
| EF |
| AB |
| FC |
| BC |
解答:解: ∵DE∥BC,
∵DE∥BC,
∴
=
,所以D选项错误;
∵EF∥AB,
∴
=
,
∴
=
,所以A选项错误,C选项正确;
∵EF∥AB,
∴
=
,
∴
=
,所以B选项错误.
故选C.
 ∵DE∥BC,
∵DE∥BC,∴
| AD |
| DB |
| AE |
| EC |
∵EF∥AB,
∴
| AE |
| EC |
| BF |
| FC |
∴
| AD |
| DB |
| BF |
| FC |
∵EF∥AB,
∴
| EF |
| AB |
| FC |
| BC |
∴
| AB |
| BC |
| EF |
| FC |
故选C.
点评:本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.

练习册系列答案
相关题目
如图,将半径为3的圆形纸片,按下列顺序折叠,若
和
都经过圆心O,则阴影部分的面积是( )

 |
| AB |
 |
| BC |

| A、π | B、2π | C、3π | D、4π |
 如图,C为线段AB的中点,点D分线段AB的长度为2:3,已知CD=1cm,求AB的长.
如图,C为线段AB的中点,点D分线段AB的长度为2:3,已知CD=1cm,求AB的长.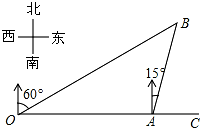 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为
如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为