题目内容
18.若|m+3|+(n-4)2=0,则m+n=1.分析 根据非负数的性质列式求出m、n的值,然后相加计算即可得解.
解答 解:∵|m+3|+(n-4)2=0,
∴m+3=0,n-4=0,
解得m=-3,n=4,
所以,m+n=(-3)+4=1.
故答案为:1.
点评 本题考查了非负数的性质:有限个非负数的和为零,那么每一个加数也必为零.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
3.某品牌电脑原价为m元,先降价n元,又降低20%,两次降价后的售价为( )
| A. | $\frac{4}{5}$(m-n)元 | B. | ($\frac{4}{5}m-n$)元 | C. | $\frac{1}{5}$(m-n)元 | D. | ($\frac{1}{5}$m-n)元 |
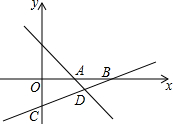 如图,直线l1:y=-x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.
如图,直线l1:y=-x+3与x轴相交于点A,直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D. 如图,请按照要求回答问题.
如图,请按照要求回答问题. 如图,AB=AC,BD⊥AC,垂足为D,CE⊥AB.垂足为E,BD和CE相交于点F,那么∠BAF与∠CAF相等吗?说明理由.
如图,AB=AC,BD⊥AC,垂足为D,CE⊥AB.垂足为E,BD和CE相交于点F,那么∠BAF与∠CAF相等吗?说明理由.