题目内容
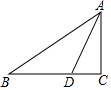
2．
如图，在△ABC中，AB=6cm，∠B=∠C=30°，那么△ABC的中线AD=（ ）cm．| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 根据等腰三角形的判定得到AB=AC，根据等腰三角形的性质得到AD⊥BC，根据直角三角形的性质即可得到结论．
解答 解：∵∠B=∠C=30°，
∴AB=AC，
∵AD是△ABC的中线，
∴AD⊥BC，
∴AD=$\frac{1}{2}$AB=3cm，
故选A．
点评 本题考查了等腰三角形的判定和性质，含30°角的直角三角形的性质，熟练掌握等腰三角形的判定和性质是解题的关键．
练习册系列答案
相关题目
19．在中国有很多吉祥的图案深受大家喜爱，人们会用这些图案来装饰生活，祈求平安．比如下列图案分别表示“福”、“禄”、“寿”、“喜”，其中既是轴对称图形，又是中心对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．
如图，△ACB中，∠ACB=Rt∠，已知∠B=α，∠ADC=β，AB=a，则BD的长可表示为（ ）
如图，△ACB中，∠ACB=Rt∠，已知∠B=α，∠ADC=β，AB=a，则BD的长可表示为（ ）| A． | a•（cosα-cosβ） | B． | $\frac{a}{tanβ-tanα}$ | ||
| C． | acosα-$\frac{a•sinα}{tanβ}$ | D． | a•cosα-asinα•a•tanβ |
10．若2x=4y+1，27y=3x+1，则x-y等于（ ）
| A． | 5 | B． | -3 | C． | -1 | D． | 1 |
17．
如图，⊙A的半径为3，圆心A的坐标为（1，0），点B（m，0）在⊙A内，则m的取值范围是（ ）
如图，⊙A的半径为3，圆心A的坐标为（1，0），点B（m，0）在⊙A内，则m的取值范围是（ ）| A． | m＜4 | B． | m＞-2 | C． | -2＜m＜4 | D． | m＜-2或m＞4 |
如图，在△ABC中，BD=CD，∠1=∠2，小颖说：“AD⊥BC”，你认为她说的对吗？说明你的理由．
14．已知a-b=2，则a2-4b-b2的值是（ ）
| A． | 0 | B． | 2 | C． | 4 | D． | 6 |
11．
如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，则下列结论错误的是（ ）
如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，则下列结论错误的是（ ）| A． | EF=2CE | B． | S△AEF=$\frac{2}{3}$S△BCF | C． | BF=3CD | D． | BC=$\frac{3}{2}$AE |
12．已知关于x的不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x-2≥3}\end{array}\right.$ 整数解有4个，则b的取值范围是（ ）
| A． | 7≤b＜8 | B． | 7≤b≤8 | C． | 8≤b＜9 | D． | 8≤b≤9 |