题目内容
11. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )| A. | EF=2CE | B. | S△AEF=$\frac{2}{3}$S△BCF | C. | BF=3CD | D. | BC=$\frac{3}{2}$AE |
分析 由平行四边形的性质可知AF∥CD,利用相似三角形的性质可求得EF=2CE,可判断A、B,利用AB=CD,可判断C,利用AD=BC可判断D,可求得答案.
解答 解:
∵四边形ABCD为平行四边形,
∴AF∥CD,
∴△AEF∽△DEC,
∴$\frac{EF}{CE}$=$\frac{AE}{DE}$=$\frac{AF}{CD}$=2,
∴EF=2CE,故A是正确的结论;
∴$\frac{EF}{CF}$=$\frac{2}{3}$,
∵AD∥BC,
∴△AEF∽△BCF,
∴$\frac{{S}_{△AEF}}{{S}_{△BCF}}$=($\frac{EF}{CF}$)2=$\frac{4}{9}$,
∴S△AEF=$\frac{4}{9}$S△BCF,故B是错误的结论;
∵$\frac{AF}{BF}$=$\frac{EF}{CF}$=$\frac{2}{3}$,
∴$\frac{BF}{AB}$=3,
∵AB=CD,
∴BF=3CD,故C是正确的结论;
∵$\frac{EF}{CF}$=$\frac{AE}{BC}$=$\frac{2}{3}$,
∴BC=$\frac{3}{2}$AE,故D是正确的结论;
故选B.
点评 本题主要考查相似三角形的判定和性质和平行四边形的性质,利用平行四边形的性质证得△AEF∽△DEC和△AEF∽△BCF是解题的关键.

练习册系列答案
相关题目
2. 如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.
如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.
 如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.
如图,在△ABC中,AB=6cm,∠B=∠C=30°,那么△ABC的中线AD=( )cm.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.若直线y=ax+b不经过第三象限,则下列不等式中,总成立的是( )
| A. | b>0 | B. | b-a<0 | C. | b-a>0 | D. | a+b>0 |
3. 下列图中,哪个可以通过如图图形平移得到( )
下列图中,哪个可以通过如图图形平移得到( )
 下列图中,哪个可以通过如图图形平移得到( )
下列图中,哪个可以通过如图图形平移得到( )| A. |  | B. |  | C. |  | D. |  |
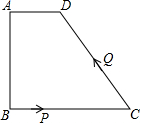 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0) 如图,长方体盒子是用大长方形硬纸片裁剪制作的,每个盒子由4个小长方形侧面和上下2个正方形底面组成,大长方形硬纸片按两种方法裁剪:A所示方法剪4个侧面:B所示方法剪6个底面.现有112张大长方形硬纸片全部用于裁剪制作长方体盒子,设裁剪时x张用A方法,其余用B方法.
如图,长方体盒子是用大长方形硬纸片裁剪制作的,每个盒子由4个小长方形侧面和上下2个正方形底面组成,大长方形硬纸片按两种方法裁剪:A所示方法剪4个侧面:B所示方法剪6个底面.现有112张大长方形硬纸片全部用于裁剪制作长方体盒子,设裁剪时x张用A方法,其余用B方法.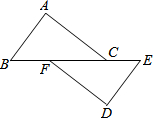 已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF.
已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF.