题目内容
代数式
+
+
的最小值是( )
| x-1 |
| x-2 |
| x+2 |
| A、0 | ||
| B、3 | ||
C、
| ||
| D、不存在 |
考点:无理函数的最值
专题:
分析:首先由代数式
+
+
的有意义,即可求得x的取值范围,然后由
,
,
都随x的增大而增大,即可得当x取最小值时,代数式
的值最小,代入即可求得答案.
| x-1 |
| x-2 |
| x+2 |
| x-1 |
| x-2 |
| x+2 |
| x+2 |
解答:解:若代数式
+
+
有意义,
则
,
解得:x≥2,
∵由
,
,
都随x的增大而增大,
∴当x=2时,代数式
的值最小,
即
+
+
=1+0+2=3.
故选:B.
| x-1 |
| x-2 |
| x+2 |
则
|
解得:x≥2,
∵由
| x-1 |
| x-2 |
| x+2 |
∴当x=2时,代数式
| x+2 |
即
| x-1 |
| x-2 |
| x+2 |
故选:B.
点评:此题考查了函数的最值问题,考查了二次根式的意义.此题难度适中,解题的关键是根据题意求得x的取值范围.

练习册系列答案
相关题目
 已知实数a、b在数轴上的对应点的位置如图,那么
已知实数a、b在数轴上的对应点的位置如图,那么| a |
| -b |
| A、非负数 | B、正数 |
| C、负数 | D、以上答案均不对 |
已知
=
+n(mn≠-1),则x=( )
| 1 |
| x |
| 1 |
| m |
A、m+
| ||
B、m-
| ||
C、
| ||
D、
|
化简:-
=( )
| 4 |
| A、2 | B、-2 | C、4 | D、-4 |
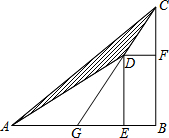 如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为何?( )
如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为何?( )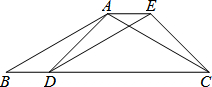 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.