题目内容
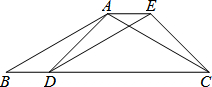 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.(1)求证:△BAD≌△ACE;
(2)若∠B=30°,∠ADC=45°,BD=4,求四边形ADCE的面积.(结果保留根号)
考点:平行四边形的性质,全等三角形的判定与性质,梯形
专题:
分析:(1)根据平行四边形的性质得出,再利用等三角形的判定方法得出即可;
(2)首先根据锐角三角函数关系得出BG=
x,进而利用BG-DG=BD求出AG的长,进而得出梯形ADCE的面积.
(2)首先根据锐角三角函数关系得出BG=
| 3 |
解答:(1)证明:∵AB=AC,
∴∠B=∠ACB.
又∵四边形ABDE是平行四边形
∴AE∥BD,AE=BD,
∴∠ACB=∠CAE=∠B,
在△DBA和△AEC中,
,
∴△DBA≌△AEC(SAS);
(2)解:过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=45°,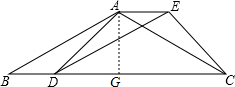
∴AG=DG=x,
在Rt△AGB中,∵∠B=30°,
∴BG=
x,
又∵BD=4.
∴BG-DG=BD,即
x-x=4,
解得AG=x=2(
+1),
∴AE+DC=BC=2BG=2(4+2
+2)=12+4
∴S梯形ADCE=
AG•(AE+DC)=
×(2
+2)×(4
+12)=24+16
.
∴∠B=∠ACB.
又∵四边形ABDE是平行四边形
∴AE∥BD,AE=BD,
∴∠ACB=∠CAE=∠B,
在△DBA和△AEC中,
|
∴△DBA≌△AEC(SAS);
(2)解:过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=45°,

∴AG=DG=x,
在Rt△AGB中,∵∠B=30°,
∴BG=
| 3 |
又∵BD=4.
∴BG-DG=BD,即
| 3 |
解得AG=x=2(
| 3 |
∴AE+DC=BC=2BG=2(4+2
| 3 |
| 3 |
∴S梯形ADCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
点评:此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,根据BG-DG=BD得出AG的长是解题关键.

练习册系列答案
相关题目
代数式
+
+
的最小值是( )
| x-1 |
| x-2 |
| x+2 |
| A、0 | ||
| B、3 | ||
C、
| ||
| D、不存在 |
 解不等式组:
解不等式组: 如图,在?ABCD中,点E、点F分别在AD、CB的延长线上,且DE=BF,连结EF分别交AB、CD于点H、点G.
如图,在?ABCD中,点E、点F分别在AD、CB的延长线上,且DE=BF,连结EF分别交AB、CD于点H、点G.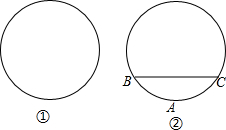 某市新建了圆形文化广场,小杰和小浩准备用不同的方法测量该广场的半径.
某市新建了圆形文化广场,小杰和小浩准备用不同的方法测量该广场的半径.