题目内容
1．
我们在求方程x2+2x-6=0的近似根时，可以将原方程变形为-$\frac{1}{2}$x2+3=x，然后在同一直角坐标系中画出函数y=-$\frac{1}{2}$x2+3和y=x的图象，发现-4＜x1＜-3，1＜x2＜2．请你利用已有的函数图象判断方程x3-6x+12=0在实数范围内有几个解？
分析 根据等式的性质，可得三次函数与一次函数，根据函数图象的交点的横坐标是方程组的解，可得答案．
解答 解：移项，得
x3=6x-12，
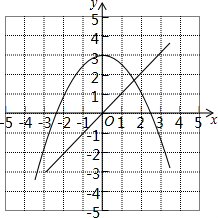
在同一平面直角坐标系内画出y=x3与y=6x-12的图象，如图
，
方程x3-6x+12=0在实数范围内有0个解．
点评 本题考查了图象法求一元二次方程的近似解，图象的交点坐标的横坐标是方程的解．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
19．
下表中的数据是使用了某种调查方法获得的：
初中男生身高情况抽样调查表
（1）根据表中的数据填写表中的空格；
（2）根据填写的数据，在右图中绘制频数分布直方图与频数分布折线图．
下表中的数据是使用了某种调查方法获得的：初中男生身高情况抽样调查表
| 年级 人数 身高（cm） | 七年级 | 八年级 | 九年级 | 总计（频数） |
| 143-153 | 12 | 3 | 0 | 15 |
| 153-163 | 18 | 9 | 6 | 33 |
| 163-173 | 24 | 33 | 39 | 96 |
| 173-183 | 6 | 15 | 12 | 33 |
| 183-193 | 0 | 0 | 3 | 3 |
| 注：每组可含最低值，不含最高值 | ||||
（2）根据填写的数据，在右图中绘制频数分布直方图与频数分布折线图．