题目内容
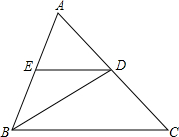如图，在△ABC中，∠AED=80°，BD是∠ABC的平分线，∠DBC=40°，求∠EDB的度数．考点：等腰三角形的判定与性质,平行线的性质
专题：
分析：首先运用角平分线的定义求得∠ABC的度数，再证得DE∥BC，再运用平行线的性质求得∠EDB．
解答：证明：∵BD是∠ABC的平分线，∠DBC=40°，
∴∠ABC=2∠DBC=80°，
∴∠AED=∠ABC，
∴DE∥BC，
∴∠EDB=∠DBC=40°．
∴∠ABC=2∠DBC=80°，
∴∠AED=∠ABC，
∴DE∥BC，
∴∠EDB=∠DBC=40°．
点评：本题主要运用了平行线的判定与性质以及角平分线的概念，比较简单．
练习册系列答案
特高级教师点拨系列答案
相关题目
王刚将一副三角板如图所示摆在一起，若已知CD=2，AB=
已知：如图，OB是∠AOC的角平分线，OC是∠AOD的角平分线，∠COD=70°，那么∠AOD的度数为
已知实a，b在数轴上的位置如图所示，化简（
如图，在Rt△ACB中，∠ACB=90°，点D是AB上一点．将△BCD沿CD折叠，使B点落在AC边上的B′处．
若∠A=20°18′，∠B=20°15″，∠C=20.25°，则有（ ）
| A、∠A＞∠B＞∠C |
| B、∠B＞∠A＞∠C |
| C、∠A＞∠C＞∠B |
| D、∠C＞∠A＞∠B |
下列图案均是用长度相同的小木棒按一定的规律拼搭而成：拼搭第1个图案需4根小木棒，拼塔第2个图案需10根小木棒，…，依此规律，拼成第6个图案小木棒（ ）
| A、36根 | B、48根 |
| C、54根 | D、64根 |