题目内容
在2014巴西世界杯的一场足球比赛中,阿根廷队梅西在距球门12米处起脚射门.已知足球运行路线是一条抛物线,运行到最高点时距地面3.2米,且此时距球门水平距离为4米,足球门高为2.44米(包括球门横梁),球门横梁直径为0.08米.

(1)如图所示,建立平面直角坐标系,求足球运行路线的抛物线的解析式;
(2)判断足球是否能射入球门?(假设守门员未能扑到此球).

(1)如图所示,建立平面直角坐标系,求足球运行路线的抛物线的解析式;
(2)判断足球是否能射入球门?(假设守门员未能扑到此球).
考点:二次函数的应用
专题:
分析:(1)根据条件可以得到抛物线的顶点坐标是(0,3.2),利用待定系数法即可求得函数的解析式;
(2)求出当x=-4时,抛物线的函数值,与2.36米进行比较即可判断.
(2)求出当x=-4时,抛物线的函数值,与2.36米进行比较即可判断.
解答:解:(1)抛物线的顶点坐标是(0,3.2),
设抛物线的解析式是:y=a(x-0)2+3.2,
把(8,0)代入得64a+3.2=0,
解得a=-0.05,
则抛物线是y=-0.05x2+3.2;
(2)∵足球门高为2.44米(包括球门横梁),球门横梁直径为0.08米.
∴足球门横梁下沿距离地面2.44-0.08=2.36,
∵当x=-4时,y=-0.05×16+3.2=2.4>2.36米.
∴未能射中球门.
设抛物线的解析式是:y=a(x-0)2+3.2,
把(8,0)代入得64a+3.2=0,
解得a=-0.05,
则抛物线是y=-0.05x2+3.2;
(2)∵足球门高为2.44米(包括球门横梁),球门横梁直径为0.08米.
∴足球门横梁下沿距离地面2.44-0.08=2.36,
∵当x=-4时,y=-0.05×16+3.2=2.4>2.36米.
∴未能射中球门.
点评:本题考查了待定系数法求二次函数的解析式,以及二次函数的应用,正确求得解析式是关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
一元二次方程2x2+2
x+1=0的根的情况是( )
| 2 |
| A、方程有两个不相等的实数根 |
| B、方程有两个相等的实数根 |
| C、方程没有实数根 |
| D、方程根的情况不能确定 |
 如图,已知△ABC中,∠C=90°,AC=BC=2
如图,已知△ABC中,∠C=90°,AC=BC=2| 2 |
A、2-
| ||||
B、
| ||||
C、2(
| ||||
| D、1 |
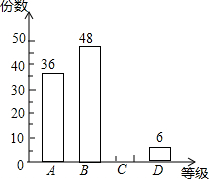 某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.
某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.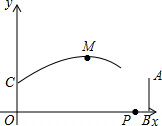 在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系.
在一次足球赛中,甲运动员在距对方球门AB正前方19.8m的点O处起跳到距地面2m的点C处接队友的传球,用头球攻对方球门,球门AB的高度为2.44m,球的运动轨迹看作抛物线的一部分,当球运动到最高点M时的高度为6m,离甲运动员起跳点O的水平距离为10m,以O为原点建立如图所示的坐标系. 如图,AB=AC,CE⊥AC,CE⊥AB,垂足分别是D,E,BD,CE相交于点M,点M在∠A的平分线上吗?证明你的结论.
如图,AB=AC,CE⊥AC,CE⊥AB,垂足分别是D,E,BD,CE相交于点M,点M在∠A的平分线上吗?证明你的结论. 如图所示,∠A=50°,∠C=80°,∠CBP=∠PBA,∠CDP=∠PDA,求∠P的度数.
如图所示,∠A=50°,∠C=80°,∠CBP=∠PBA,∠CDP=∠PDA,求∠P的度数.