题目内容
12. 如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )| A. | a | B. | 2a | C. | $\frac{3}{2}$a | D. | $\frac{5}{2}$a |
分析 先根据锐角三角函数的定义求出BC的长,进而可得出结论.
解答 解:∵CD=$\sqrt{2}$a,∠D=45°,AB⊥BD,
∴BC=CD•sin45°=$\sqrt{2}$a•$\frac{\sqrt{2}}{2}$=a.
∵点C是AB的中点,
∴AB=2BC=2a.
故选B.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
2.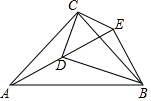 如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
 如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )
如图,已知△ABC是等腰直角三角形,其内部有一点D,连接BD,以BD为斜边作等腰直角三角形BDE,连接AD、CD、CE,若CD=1,AD=2,∠DCE=90°,则DE的长是 ( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
3.为了解某市参加中考的40073名学生的身高情况,抽查了其中1000名学生的身高进行统计分析.下面叙述正确的是( )
| A. | 40073名学生是总体 | |
| B. | 每名学生是总体的一个个体 | |
| C. | 本次调查是全面调查 | |
| D. | 1000名学生的身高是总体的一个样本 |
7.已知⊙A的半径长为2,⊙B的半径长为5,如果⊙A与⊙B内含,那么圆心距AB的长度可以为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
4.口袋中装有形状、大小与质地都相同的红球2个,黄球1个,下列事件为随机事件的是( )
| A. | 随机摸出1个球,是白球 | B. | 随机摸出1个球,是红球 | ||
| C. | 随机摸出1个球,是红球或黄球 | D. | 随机摸出2个球,都是黄球 |
2.已知一次函数y1=-ax+3(a为常数)的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象在第三相交于点A(a,$\frac{a}{2}$),则y2的解析式是( )
| A. | ${y_2}=\frac{9}{8x}$ | B. | ${y_2}=\frac{1}{2x}$ | C. | ${y_2}=\frac{2}{x}$ | D. | ${y_2}=-\frac{2}{x}$ |

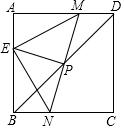 正方形ABCD中,点P是对角线BD的中点,过P点的直线分别交边AD,BC于M,N,EP⊥MN交边AB于点E.
正方形ABCD中,点P是对角线BD的中点,过P点的直线分别交边AD,BC于M,N,EP⊥MN交边AB于点E. 如图是由3个大小相同的小立方块搭成的几何体,这个几何体的俯视图是( )
如图是由3个大小相同的小立方块搭成的几何体,这个几何体的俯视图是( )


