题目内容
2．
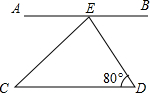如图，AB∥CD，CE平分∠AED，则∠C=（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 55° |
分析 根据平行线的性质和角平分线的定义即可得到结论．
解答 解：∵AB∥CD，
∴∠AED=180°-∠D=100°，
∵CE平分∠AED，
∴∠AEC=$\frac{1}{2}∠$AED=50°，
∵AB∥CD，
∴∠C=∠AED=50°，
故选C．
点评 本题考查了平行线的性质，角平分线的定义，熟练掌握平行线的性质是解题的关键．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
如图，⊙O中，直径AB与弦CD相交，E是AC延长线上一点，连接BC、BD，且∠EBC=∠D．
13．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资成本x成正比例关系，种植花卉的利润y2与投资成本x的平方成正比例关系，并得到了表格中的数据；
（1）分别求出利润y1与y2关于投资量x的函数关系式；
（2）如果这位专业户计划以8万元资金投入种植花卉和树木，设他投入种植花卉金额万元，种植花卉和树木共获利润W万元，求出W与m之间的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
（3）若该专业户想获利不低于22万元，在（2）的条件下，求出投资种植花卉的金额m的范围．
| 投资量x（万元） | 2 |
| 种植树木的利润y1（万元） | 4 |
| 种植花卉的利润y2（万元） | 2 |
（2）如果这位专业户计划以8万元资金投入种植花卉和树木，设他投入种植花卉金额万元，种植花卉和树木共获利润W万元，求出W与m之间的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
（3）若该专业户想获利不低于22万元，在（2）的条件下，求出投资种植花卉的金额m的范围．
10．
问题情境
已知矩形的面积为S（S为常数，S＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+$\frac{S}{x}$）（x＞0）
探索研究
我们可以借鉴学习函数的经验，先探索函数y=x+$\frac{1}{x}$（x＞0）的图象性质．
①列表：
表中m=$\frac{10}{3}$；
②描点：如图所示；
③连线：请在图中画出该函数的图象；
④观察图象，写出两条函数的性质；函数有最小值2；当x＞1时，y随x的增大而增大
解决问题
在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．同样通过配方也可以求函数y=x+$\frac{1}{x}$（x＞0）的最小值．
y=x+$\frac{1}{x}$=${（\sqrt{x}）}^{2}$+${（\sqrt{\frac{1}{x}}）}^{2}$=${（\sqrt{x}）}^{2}$+${（\sqrt{\frac{1}{x}}）}^{2}$-2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$+2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$=${（\sqrt{x}-\sqrt{\frac{1}{x}）}}^{2}$+2
∵${（{\sqrt{x}-\sqrt{\frac{1}{x}}}）^2}$≥0，∴y≥2
∴当$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=0，即x=1时，y最小值=2
请类比上面配方法，直接写出“问题情境”中的问题答案．
问题情境已知矩形的面积为S（S为常数，S＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+$\frac{S}{x}$）（x＞0）
探索研究
我们可以借鉴学习函数的经验，先探索函数y=x+$\frac{1}{x}$（x＞0）的图象性质．
①列表：
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{4}$ | m | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | $\frac{17}{4}$ | … |
②描点：如图所示；
③连线：请在图中画出该函数的图象；
④观察图象，写出两条函数的性质；函数有最小值2；当x＞1时，y随x的增大而增大
解决问题
在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．同样通过配方也可以求函数y=x+$\frac{1}{x}$（x＞0）的最小值．
y=x+$\frac{1}{x}$=${（\sqrt{x}）}^{2}$+${（\sqrt{\frac{1}{x}}）}^{2}$=${（\sqrt{x}）}^{2}$+${（\sqrt{\frac{1}{x}}）}^{2}$-2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$+2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$=${（\sqrt{x}-\sqrt{\frac{1}{x}）}}^{2}$+2
∵${（{\sqrt{x}-\sqrt{\frac{1}{x}}}）^2}$≥0，∴y≥2
∴当$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=0，即x=1时，y最小值=2
请类比上面配方法，直接写出“问题情境”中的问题答案．
7．已知⊙A的半径长为2，⊙B的半径长为5，如果⊙A与⊙B内含，那么圆心距AB的长度可以为（ ）
| A． | 0 | B． | 3 | C． | 6 | D． | 9 |
11．在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A（x1，y1）、B（x2，y2）．若x1＜0＜x2，y1＜y2则k的取值范围是（ ）
| A． | k≥$\frac{1}{3}$ | B． | k＞$\frac{1}{3}$ | C． | k＜-$\frac{1}{3}$ | D． | k＜$\frac{1}{3}$ |
12．在平面直角坐标系中，点A（4，-2），B（0，2），C（a，-a），a为实数，当△ABC的周长最小时，a的值是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | $\sqrt{2}$ |