题目内容
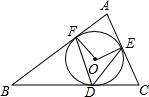 如图,⊙O内切于△ABC,切点为D、E、F,∠B=45°,∠C=55°,连接OE、OF、OE、OF,则∠EDF等于( )
如图,⊙O内切于△ABC,切点为D、E、F,∠B=45°,∠C=55°,连接OE、OF、OE、OF,则∠EDF等于( )| A、45° | B、55° |
| C、50° | D、70° |
考点:三角形的内切圆与内心
专题:
分析:根据三角形内角和定理求出∠A,根据切线性质求出∠OFA=∠OEA=90°,求出∠EOF,根据圆周角定理得出∠EDF=
∠EOF,代入求出即可.
| 1 |
| 2 |
解答:解:∵在△ABC中,∠B=45°,∠C=55°,
∴∠A=180°-45°-55°=80°,
∵⊙O内切于△ABC,切点为D、E、F,
∴∠OFA=∠OEA=90°,
∴∠EOF=360°-90°-80°-90°=100°,
∴∠EDF=
∠EOF=50°,
故选C.
∴∠A=180°-45°-55°=80°,
∵⊙O内切于△ABC,切点为D、E、F,
∴∠OFA=∠OEA=90°,
∴∠EOF=360°-90°-80°-90°=100°,
∴∠EDF=
| 1 |
| 2 |
故选C.
点评:本题考查了圆周角定理,切线性质,三角形内切圆,多边形的内角和定理的应用,解此题的关键是求出∠FOE的度数,题目比较好,难度适中.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
已知关于x的不等式组
无解,则m取值范围是( )
|
| A、m<2 | B、m≤2 |
| C、m>2 | D、m≥2 |
如果(am•b•bn)3=a6b15,那么m,n的值分别是( )
| A、2,4 | B、2,5 |
| C、3,5 | D、3,-5 |
下列运算正确的是( )
| A、-(a-1)=-a-1 |
| B、(2a3)2=4a6 |
| C、(a-b)2=a2-b2 |
| D、a3+a2=2a5 |
方程
=
的解为( )
| 2 |
| x |
| 1 |
| 1-x |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知某条经过原点的直线还经过点(2,1),下列结论正确的是( )
| A、直线的解析式为y=2x |
| B、函数图象经过二、四象限 |
| C、函数图象一定经过点(-2,-1) |
| D、y随x的增大而减小 |
如果点P(5,y)在第四象限,则y的取值范围是( )
| A、y<0 |
| B、y>0 |
| C、y大于或等于0 |
| D、y小于或等于0 |
 如图5,A为反比例函数y=
如图5,A为反比例函数y= 如图,C是线段AB的中点,AE⊥AB,BF⊥AB,过点C的直线与AE、BF分别交于点E、F.
如图,C是线段AB的中点,AE⊥AB,BF⊥AB,过点C的直线与AE、BF分别交于点E、F.