题目内容
某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.现在要使利润为6125元,每件商品应降价( )元.
| A、3 | B、2.5 | C、2 | D、5 |
考点:一元二次方程的应用
专题:
分析:设应降价x元,根据每降价1元,每星期可多卖出20件,利润为6125元列出方程,求出x的值即可.
解答:解:设应降价x元,根据题意得:
(300+20x)(60-40-x)=6125,
解得:x1=x2=2.5,
则每件商品应降价2.5元;
故选B.
(300+20x)(60-40-x)=6125,
解得:x1=x2=2.5,
则每件商品应降价2.5元;
故选B.
点评:本题考查了一元二次方程的应用.此题找到关键描述语,找到等量关系准确的列出方程是解决问题的关键,本题的等量关系是降价x元后,利润为6125元.

练习册系列答案
相关题目
下列运算正确的是( )
| A、-(a-1)=-a-1 |
| B、(2a3)2=4a6 |
| C、(a-b)2=a2-b2 |
| D、a3+a2=2a5 |
某车间有28名工人生产螺丝和螺母,已知平均每人每天可生产螺丝12个或螺母18个,一个螺丝配两个螺母.若安排x名工人生产螺丝,y名工人生产螺母才能使每天生产的正品正好配套,则可得方程组( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的半径为( )
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器厚度,则球的半径为( )| A、5cm | B、6cm |
| C、7cm | D、8cm |
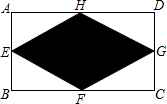 已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为( )
已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为( )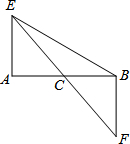 如图,C是线段AB的中点,AE⊥AB,BF⊥AB,过点C的直线与AE、BF分别交于点E、F.
如图,C是线段AB的中点,AE⊥AB,BF⊥AB,过点C的直线与AE、BF分别交于点E、F.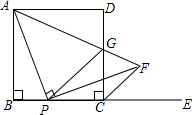 如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
如图,在正方形ABCD中,AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.